沪科版九年级上第一次月考
试卷更新日期:2020-04-13 类型:月考试卷
一、选择题
-
1. 抛物线y=3(x﹣2)2+5的顶点坐标是( )A、(﹣2,5) B、(﹣2,﹣5) C、(2,5) D、(2,﹣5)2. 点(2,﹣4)在反比例函数y= 的图象上,则下列各点在此函数图象上的是( )A、(2,4) B、(﹣1,﹣8) C、(﹣2,﹣4) D、(4,﹣2)3. 对于函数y=﹣2(x﹣m)2的图象,下列说法错误的是( )A、开口向下 B、对称轴是x=m C、最大值为0 D、与y轴不相交4. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
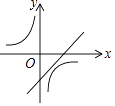 B、
B、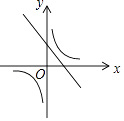 C、
C、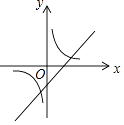 D、
D、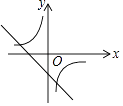 5. 已知二次函数y=x2﹣x+ m﹣1的图象与x轴有交点,则m的取值范围是( )A、m≤5 B、m≥2 C、m<5 D、m>26. 将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度,得到的函数表达式是( )
5. 已知二次函数y=x2﹣x+ m﹣1的图象与x轴有交点,则m的取值范围是( )A、m≤5 B、m≥2 C、m<5 D、m>26. 将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度,得到的函数表达式是( )
A、y=(x+3)2﹣2 B、y=(x+3)2+2 C、y=(x﹣1)2+2 D、y=(x﹣1)2﹣27. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、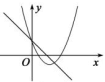 B、
B、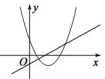 C、
C、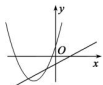 D、
D、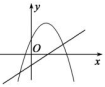 8. 如图,正比例函y1=k1x与反比例函数y2= 的图象相交于A、B两点,其中点A的横坐标为1.当y1<y2时,x的取值范围是( )
8. 如图,正比例函y1=k1x与反比例函数y2= 的图象相交于A、B两点,其中点A的横坐标为1.当y1<y2时,x的取值范围是( )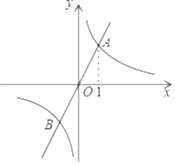 A、x<﹣1或x>1 B、﹣1<x<0或x>1 C、﹣1<x<0或0<x<1 D、x<﹣1或0<x<l9. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
A、x<﹣1或x>1 B、﹣1<x<0或x>1 C、﹣1<x<0或0<x<1 D、x<﹣1或0<x<l9. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )
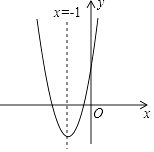 A、1个 B、2个 C、3个 D、4个10. 反比例函数y= 图象上三个点的坐标为(x1 , y1)、(x2 , y2)、(x3 , y3),若x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是 ( )A、y1<y2<y3 B、y2<y1<y3 C、y2<y3<y1 D、y1<y3<y2
A、1个 B、2个 C、3个 D、4个10. 反比例函数y= 图象上三个点的坐标为(x1 , y1)、(x2 , y2)、(x3 , y3),若x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是 ( )A、y1<y2<y3 B、y2<y1<y3 C、y2<y3<y1 D、y1<y3<y2二、填空题
-
11. 如图,点A是反比例函数y1= (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 .
 12. 已知二次函数y=x2﹣4x+k的图象的顶点在x轴下方,则实数k的取值范围是 .
12. 已知二次函数y=x2﹣4x+k的图象的顶点在x轴下方,则实数k的取值范围是 .
13. 如图,一次函数y=x﹣2的图象与反比例函数y= (k>0)的图象相交于A.B两点,与x轴交于点C,若tan∠AOC= ,则k的值为 .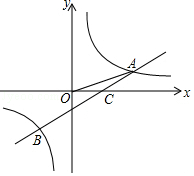 14. 已知:点P(m,n)在直线y=﹣x+2上,也在双曲线y=﹣ 上,则m2+n2的值为 。15. 对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ,﹣ }=;若min{(x﹣1)2 , x2}=1,则x= .
14. 已知:点P(m,n)在直线y=﹣x+2上,也在双曲线y=﹣ 上,则m2+n2的值为 。15. 对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ,﹣ }=;若min{(x﹣1)2 , x2}=1,则x= .
16. 数y=ax2+bx+c(a<0)图象与x轴的交点A.B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:①16a﹣4b+c<0;②若P(﹣5,y1),Q( ,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣ .其中正确的有(请将结论正确的序号全部填上)
三、解答题
-
17. 设反比例函数的解析式为y= (k>0).
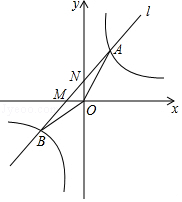 (1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.18. 销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.(1)、写出y与x中间的函数关系书和自变量x的取值范围;(2)、超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?19. (1, )是反比例函数图象上的一点,直线AC经过坐标原点且与反比例函数图象的另一支交于点C , 求C的坐标及反比例函数的表达式.20. 以下材料,然后解答问题:材料:将二次函数y=﹣x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).21. 一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.18. 销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.(1)、写出y与x中间的函数关系书和自变量x的取值范围;(2)、超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?19. (1, )是反比例函数图象上的一点,直线AC经过坐标原点且与反比例函数图象的另一支交于点C , 求C的坐标及反比例函数的表达式.20. 以下材料,然后解答问题:材料:将二次函数y=﹣x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).21. 一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.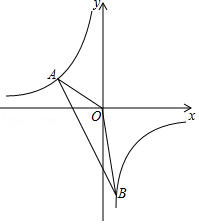 (1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积.22. 物线与x轴交于A.B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x=-
(1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积.22. 物线与x轴交于A.B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x=-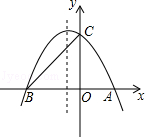 (1)、求抛物线的解析式;(2)、M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.23. 于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.(1)、求证:无论k为何值,方程总有两个不相等实数根;(2)、已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;(3)、若原方程的一个根大于3,另一个根小于3,求k的最大整数值.24. 种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
(1)、求抛物线的解析式;(2)、M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.23. 于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.(1)、求证:无论k为何值,方程总有两个不相等实数根;(2)、已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;(3)、若原方程的一个根大于3,另一个根小于3,求k的最大整数值.24. 种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:销售第x天
第1天
第2天
第3天
第4天
…
第30天
销售单价m(元/件)
49
48
47
46
…
20
日销售量n(件)
45
50
55
60
…
190
(1)、观察表中数据,分别直接写出m与x,n与x的函数关系式: , 。(2)、求商场销售该商品第几天时该商品的日销售额恰好为3600元?(3)、销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?25. 在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.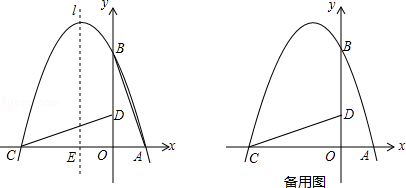 (1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其坐标为t,
(1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.