第23章解直角三角形单元检测A卷

试卷更新日期：2020-04-13 类型：单元试卷

进入出卷网下载

一、选择题

1.
如图，在Rt△ABC中，∠C=90°，AB=6，cosB= $\frac{2}{3}$ ，则BC的长为（）

A、4 B、2 $\sqrt{5}$ C、 $\frac{18 \sqrt{13}}{13}$ D、 $\frac{12 \sqrt{13}}{13}$

查看试题解析
2. 在Rt△ABC中，∠C=90°，sinA= $\frac{4}{5}$ ，AC=6cm，则BC的长度为（　　）

A、6cm B、7cm C、8cm D、9cm

查看试题解析
3. 如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的（）

A、 $\frac{B D}{B C}$ B、 $\frac{B C}{A B}$ C、 $\frac{A D}{A C}$ D、 $\frac{C D}{A C}$

查看试题解析
4. 如图，将∠AOB放置在5×5的正方形网格中，则tan∠AOB的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{2 \sqrt{13}}{13}$ D、 $\frac{3 \sqrt{13}}{13}$

查看试题解析
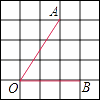5. 在△ABC中，∠C＝90°，BC＝2，AB＝4，则下列结论中错误的是（）

A、sinA＝ $\frac{1}{2}$ B、∠B＝60° C、tanB＝ $\frac{\sqrt{3}}{3}$ D、cosB＝ $\frac{1}{2}$

查看试题解析
6. “奔跑吧，兄弟！”节目组，预设计一个新的游戏：“奔跑”路线需经A、B、C、D四地．如图，其中A、B、C三地在同一直线上，D地在A地北偏东30°方向、在C地北偏西45°方向．C地在A地北偏东75°方向．且BD=BC=30m．从A地到D地的距离是（）

A、30 $\sqrt{3}$ m B、20 $\sqrt{5}$ m C、30 $\sqrt{2}$ m D、15 $\sqrt{6}$ m

查看试题解析
7. 如图，是交警部门为缓解市区内交通拥挤在学府路某处设立的路况显示牌．立杆AB的高度是 $\sqrt{3}$ 米，从D点测得显示牌顶端C和底端B的仰角分别是60°和45°，则显示牌BC的高度为（）

A、 $\sqrt{3}$ 米 B、(3－ $\sqrt{3}$ )米 C、9米 D、(2 $\sqrt{3}$ －3)米

查看试题解析
8.
某市在“旧城改造”中计划在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（）

A、450a元 B、225a元 C、150a元 D、300a元

查看试题解析
9. 如图所示，在△ABC中，∠C＝90°，AC＝16cm，AB的垂直平分线MN交AC于D，连接BD，若 $\cos ∠ B D C = \frac{3}{5}$ ，则BD的长是（）．

A、4cm B、6cm C、8cm D、10cm

查看试题解析
10. 在直角△ABC中，∠C=90°，∠A、∠B与∠C的对边分别是a、b和c，那么下列关系中，正确的是（）

A、cosA= $\frac{a}{c}$ B、tanA= $\frac{b}{a}$ C、sinA= $\frac{a}{c}$ D、cosA= $\frac{a}{b}$

查看试题解析
11. 如图，在 $△ A B C$ 中，点D在BC上，且BD=2CD， $A B ⊥ A D$ ，若 $\tan B = \frac{4}{3}$ ，则 $\tan ∠ C A D$ （）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{1}{4}$ C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
12. 在△ABC中，AB=12 $\sqrt{2}$ ， AC=13，cos∠B= $\frac{\sqrt{2}}{2}$ ，则BC边长为（　　）

A、7 B、8 C、8或17 D、7或17

查看试题解析

二、填空题

13.
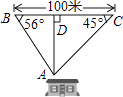
如图，为保护门源百里油菜花海，由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB，AC．若∠B=56°，∠C=45°，则游客中心A到观景长廊BC的距离AD的长约为米．（sin56°≈0.8，tan56°≈1.5）

查看试题解析
14. 如图，某公园入口处原有三阶台阶，每级台阶高为 $20 cm$ ，深为 $30 cm$ ．为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为 $A$ ，斜坡的起始点为 $C$ ，现将斜坡的坡度设计为 $i = 1 ： 4.5$ ，则 $AC$ 的长为 $cm$ ．

查看试题解析
15. 如图，河堤横断面如图所示，迎水坡AB的坡比为1： $\sqrt{3}$ ，则坡角∠A的度数为

查看试题解析
16. 如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tanB＝

查看试题解析
17. 如图所示的网格是正方形网格，∠BAC∠DAE．（填“＞”，“=”或“＜”）

查看试题解析
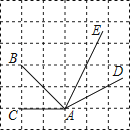18. 为加强防汛工作，某市对一拦水坝进行加固，如图，加固前拦水坝的横断面是梯形ABCD．已知迎水坡面AB=12米，背水坡面CD= $12 \sqrt{3}$ 米，∠B=60°，加固后拦水坝的横断面为梯形ABED，tanE= $\frac{3 \sqrt{3}}{13}$ ，
则CE的长为米．

查看试题解析

三、解答题

19. 计算：（ $\frac{1}{2}$ ）^﹣1﹣ $\sqrt[3]{- 8}$ +| $\sqrt{3}$ ﹣2|+2sin60°．

查看试题解析
20. 热气球的探测器显示，从热气球A看一栋楼顶部B的仰角α为45°，看这栋楼底部C的俯角β为60°，热气球与楼的水平距离为100m，求这栋楼的高度（结果保留根号）．

查看试题解析
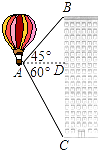21. 为了计算湖中小岛上凉亭P到岸边公路l的距离，某数学兴趣小组在公路l上的点A处，测得凉亭P在北偏东60°的方向上；从A处向正东方向行走200米，到达公路l上的点B处，再次测得凉亭P在北偏东45°的方向上，如图所示.求凉亭P到公路l的距离.（结果保留整数，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
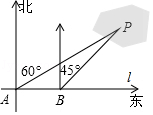22. 如图，地面上两个村庄C、D处于同一水平线上，一飞行器在空中以6千米/小时的速度沿MN方向水平飞行，航线MN与C、D在同一铅直平面内．当该飞行器飞行至村庄C的正上方A处时，测得∠NAD=60°；该飞行器从A处飞行40分钟至B处时，测得∠ABD=75°．求村庄C、D间的距离（ $\sqrt{3}$ 取1.73，结果精确到0.1千米）

查看试题解析
23. 某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°．求路况指示牌DE的高度．（精确到0.01米）

查看试题解析
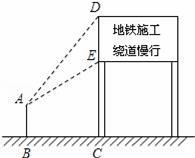24. A，B两地被大山阻隔，若要从A地到B地，只能沿着如图所示的公路先从A地到C地，再由C地到B地．现计划开凿隧道A，B两地直线贯通，经测量得：∠CAB=30°，∠CBA=45°，AC=20km，求隧道开通后与隧道开通前相比，从A地到B地的路程将缩短多少？（结果精确到0.1km，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
25. 拉杆旅行箱为人们的出行带来了极大的方便，右图是一种拉杆旅行箱的侧面示意图，箱体ABCD可视为矩形，其中AB为50cm，BC为30cm，点A到地面的距离AE为4cm，旅行箱与水平面AF成60°角，求箱体的最高点C到地面的距离．

查看试题解析
26. 如图，在△ABC中，∠C=90°，AC=3，BC=4，点D，E分别在AC，BC上（点D与点A，C不重合），且∠DEC=∠A，将△DCE绕点D逆时针旋转90°得到△DC′E′．当△DC′E′的斜边、直角边与AB分别相交于点P，Q（点P与点Q不重合）时，设CD=x，PQ=y．

(1)、求证：∠ADP=∠DEC；

(2)、求y关于x的函数解析式，并直接写出自变量x的取值范围．

查看试题解析