2018-2019沪科版九年级中期试卷
试卷更新日期:2020-04-13 类型:期中考试
一、选择题
-
1. 下列函数中,二次函数是( )A、y=﹣4x+5 B、y=x(2x﹣3) C、y=(x+4)2﹣x2 D、y=2. 在比例尺是1:40000的地图上,若某条道路长约为5cm,则它的实际长度约为( )
A、0.2km B、2km C、20km D、200km3. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )A、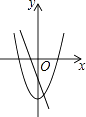 B、
B、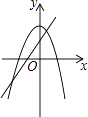 C、
C、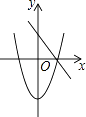 D、
D、 4. 如图,△ABC中,AB=4,BC=6.点D,点E分别是边AB,BC上的两个动点,若按照下列条件将△ABC沿DE剪开,剪下的△BDE与原三角形不相似的是( )
4. 如图,△ABC中,AB=4,BC=6.点D,点E分别是边AB,BC上的两个动点,若按照下列条件将△ABC沿DE剪开,剪下的△BDE与原三角形不相似的是( )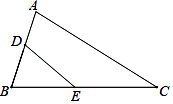 A、∠BDE=∠C B、DE∥AC C、AD=3,BE=2 D、AD=1,CE=45. 抛物线y=x2+2x+m﹣1与x轴有两个不同的交点,则m的取值范围是( )A、m<2 B、m>2 C、0<m≤2 D、m<﹣26. 如图,l1∥l2∥l3 , 则下列等式错误的是( )
A、∠BDE=∠C B、DE∥AC C、AD=3,BE=2 D、AD=1,CE=45. 抛物线y=x2+2x+m﹣1与x轴有两个不同的交点,则m的取值范围是( )A、m<2 B、m>2 C、0<m≤2 D、m<﹣26. 如图,l1∥l2∥l3 , 则下列等式错误的是( ) A、 B、 C、 D、7. 若 = ,则 的值等于( )A、 B、 C、 D、8. 下列三种方法:①相似三角形对应高的平分线的比等于相似比;②相似三角形对应高的比等于周长比;③周长之比等于1的两个三角形全等,其中正确的说法有( )A、1个 B、2个 C、3个 D、0个9. 二次函数y=﹣(x﹣1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A、 B、 C、 D、7. 若 = ,则 的值等于( )A、 B、 C、 D、8. 下列三种方法:①相似三角形对应高的平分线的比等于相似比;②相似三角形对应高的比等于周长比;③周长之比等于1的两个三角形全等,其中正确的说法有( )A、1个 B、2个 C、3个 D、0个9. 二次函数y=﹣(x﹣1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A、 B、2 C、 D、10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①因为a>0,所以函数y有最大值;②该函数的图象关于直线x=﹣1对称;③当x=﹣2时,函数y的值等于0;④当x=﹣3或x=1时,函数y的值都等于0.其中符合题意结论的个数是( )
 A、4 B、3 C、2 D、111. 函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A、4 B、3 C、2 D、111. 函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A、x<﹣4或x>2 B、﹣4<x<2 C、x<0或x>2 D、0<x<212. 二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣2,0),(x0 , 0),1<x0<2,与y轴的负半轴相交,且交点在(0,﹣2)的上方,下列结论:①b>0;②2a<b;③2a﹣b﹣1<0;④2a+c<0.其中符合题意结论的个数是( )A、1 B、2 C、3 D、4二、填空题
-
13. 如图中两三角形相似,则x= .
 14. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 = .
14. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 = .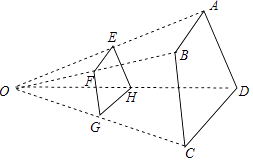 15. 函数 的图象是抛物线,则m= .16. 在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为 .17. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有 .
15. 函数 的图象是抛物线,则m= .16. 在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为 .17. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有 .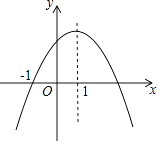 18. 如图,在矩形ABCD中, ,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
18. 如图,在矩形ABCD中, ,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:①∠AEB=∠AEH ②DH= ③ ④
其中符合题意命题的序号是(填上所有符合题意命题的序号).

三、解答题
-
19. 已知a:b:c=2:4:5,且2a﹣b+3c=15,求3a+b﹣2c的值.
20. 如图,已知以点A、D、E为顶点的三角形与△ABC相似,且AD=3,DE=2.5,AE=4,AC=6,∠AED=∠B,求△ABC的周长.
 21. 在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.(1)、求y与x满足的函数关系式(不要求写出x的取值范围);(2)、在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?22. 如图,在矩形ABCD中,DG⊥AC,垂足为G.
21. 在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.(1)、求y与x满足的函数关系式(不要求写出x的取值范围);(2)、在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?22. 如图,在矩形ABCD中,DG⊥AC,垂足为G. (1)、△ADG与△AC
(1)、△ADG与△ACD、△CDG与△CAD相似吗?为什么?
(2)、若AG=6,CG=12,求矩形ABCD的面积.23. 如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离(千米)与时间(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ,点 坐标为 ,曲线 可用二次函数 ( ,是常数)刻画.
(1)、求 的值,并求出潮头从甲地到乙地的速度;(2)、11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)、相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 , 是加速前的速度)24. 如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.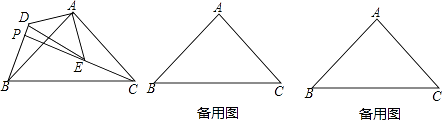 (1)、求证:BD=CE;(2)、若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;25. 在平面直角坐标系中,Rt△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1).
(1)、求证:BD=CE;(2)、若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;25. 在平面直角坐标系中,Rt△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1). (1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到x轴的距离为1的点,点B关于抛物线的对称轴l的对称点为B1 , 求点P的坐标和△B1PB的面积.26. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到x轴的距离为1的点,点B关于抛物线的对称轴l的对称点为B1 , 求点P的坐标和△B1PB的面积.26. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.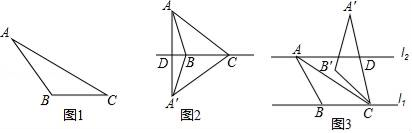 (1)、概念理解:
(1)、概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求 的值.
(3)、应用拓展:如图3,已知l1∥l2 , l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.