吉林省长春市二道区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元一次方程的是（）

A、 $x^{2} + x - 3 = x (x + 2)$ B、 $x + (4 - x) = 0$ C、 $x + y = 1$ D、 $\frac{1}{y} + x = 0$

查看试题解析
2. 方程 $3 x + 2 = 2 x - 1$ 的解为（）

A、 $x = - 3$ B、 $x = - 1$ C、 $x = 1$ D、 $x = 3$

查看试题解析
3. 不等式 $x - 1 > 2$ 的解集是（）

A、 $x > 1$ B、 $x > 2$ C、 $x > 3$ D、 $x < 3$

查看试题解析
4. 下列三条线段不能构成三角形的是（）

A、4cm、2cm、5cm B、3cm、3cm、5cm C、2cm、4cm、3cm D、2cm、2cm、6cm

查看试题解析
5. 下列图形具有稳定性的是（　　）

A、正方形 B、矩形 C、平行四边形 D、直角三角形

查看试题解析
6. 已知 ${\begin{array}{l} a + 2 b = 4 \\ 3 a + 2 b = 8 \end{array}$ ，则a＋b等于（）

A、3 B、 $\frac{8}{3}$ C、2 D、1

查看试题解析
7. 正多边形的一个内角等于144°,则该多边形的边数是（）

A、10 B、9 C、12 D、8

查看试题解析
8. 如图①是3×3正方形方格，将其中两个方格涂黑，并且使得涂黑后的整个图案是轴对称图形，约定绕正方形ABCD的中心旋转能重合的图案都视为同一种，例②中四幅图就视为同一种，则得到不同共有（）

A、4种 B、5种 C、6种 D、7种

查看试题解析

二、填空题

9. 把 $4 x - y - 1 = 0$ 写成用含 $x$ 的代数式来表示 $y ，$ 则 $y =$ .

查看试题解析
10. 如果将一副三角板按如图方式叠放，那么∠1=。

查看试题解析
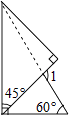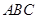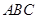11. 如图，△ 是等边三角形，点是△ 内一点。△ 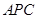按顺时针方向旋转后与△ 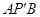重合，则旋转中心是，最小旋转角等于°

查看试题解析
12. 一个两位数，个位数字与十位数字之和为12，如果交换个位数字与十位数字的位置，所得新数比原数大36，则原两位数为.

查看试题解析
13. 如图，将直径为1个单位长度的圆从原点处沿着数轴无滑动的逆时针滚动一周，使圆上的点A从原点运动至数轴上的点B ，则点B表示的数是.

查看试题解析
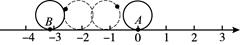14. 如图，A、B、C分别是线段 $A_{1} B 、 B_{1} C 、 C_{1} A$ 的中点，若 $△ A_{1} B_{1} C_{1}$ 的面积是14，那么△ABC的面积是.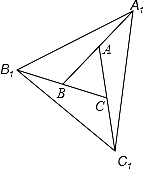

查看试题解析

三、解答题

15. 解方程: $5 (x - 5) - 2 (12 - x) = 0$

查看试题解析
16. 解方程： $\frac{2 x + 1}{4} - 1 = x - \frac{10 x + 1}{12}$ .

查看试题解析
17. 在 $y = k x + b$ 中，当 $x = 1$ 时， $y = 4$ ，当 $x = 2$ 时， $y = 10$ ，求 $k$ 和 $b$ 的值．

查看试题解析
18. 已知三角形的两边a=3，b=7，第三边是c．

(1)、第三边c的取值范围是．

(2)、若第三边c的长为偶数，则c的值为．

(3)、若a＜b＜c，则c的取值范围是．

查看试题解析
19. 如图，已知△ABC是直角三角形，DE⊥AC于点E，DF⊥BC于点F.

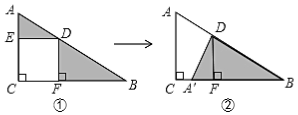(1)、请简述图①变换为图②的过程；

(2)、若AD=3，DB=4，则△ADE与△BDF的面积之和为.

查看试题解析
20. 为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完.这两种节能灯的进价、售价如表所示：

(1)、求幸福商场甲、乙两种节能灯各购进了多少只?

(2)、全部售完100只节能灯后，商场共计获利多少元?

查看试题解析
21. 一个正多边形中，一个内角的度数是它相邻的一个外角的度数的3倍.

(1)、求这个多边形的每一个外角的度数；

(2)、求这个多边形的边数.

查看试题解析
22. 如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．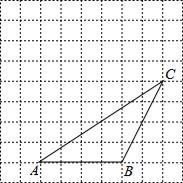

(1)、请在图中画出平移后的△A′B′C′；

(2)、再在图中画出△ABC的高CD；

(3)、在图中能使S_△_PBC＝S_△_ABC的格点P的个数有个(点P异于A)

查看试题解析
23. 甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案.在甲商场累计购物超过200元，超出200元的部分按80%收费；在乙商场累计购物超过100元，超出100元的部分按85%收费，已知小红在同一商场累计购物 $x$ 元，其中 $x > 200.$

(1)、当 $x = 300$ 时，小红在甲商场需花费元，在乙商场需花费元；

(2)、分别用含 $x$ 的代数式表示小红在甲、乙商场的实际花费；

(3)、当小红在同一商场累计购物超过200元时，通过计算说明小红在哪家商场购物的实际花费少.

查看试题解析
24. 如图1，∠MON=90°，点A、B分别在OM、ON上运动(不与点O重合).

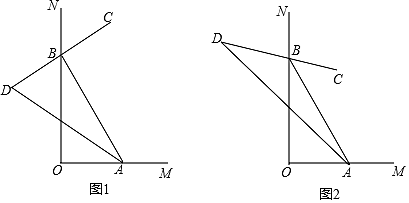(1)、若BC是∠ABN的平分线，BC的反向延长线与∠BAO的平分线交于点D，
若∠BAO=60°，则∠D=°；

(2)、猜想：∠D的度数是否随A、B的移动发生变化？并说明理由；

(3)、若∠ABC= $\frac{1}{3}$ ∠ABN，∠BAD= $\frac{1}{3}$ ∠BAO，则∠D=°；

查看试题解析