广东省深圳市宝安区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-04-13 类型:期中考试
一、单选题
-
1. 下列说法中,错误的是( )A、对顶角相等 B、同位角相等 C、等角的余角相等 D、垂线段最短2. 某种细菌的半径是0.000 0036毫米,这个数用科学记数法可表示为( )A、3.6×10﹣6毫米 B、3.6×10﹣5毫米 C、0.36×10﹣7毫米 D、36×10﹣4毫米3. 下列运算正确的是( )A、a2•a3=a5 B、a6•a3=a18 C、(a3)2=a5 D、a5+a5=a104. 若有四根木棒,长度分别为4,5,6,9(单位:cm),从中任意选取三根首尾顺次连接围成不同的三角形,下列不能围成三角形的是( )A、4,5,6 B、4,6,9 C、5,6,9 D、4,5,95. 下列各题中,适合用平方差公式计算的是( )A、(3a+b)(3b-a) B、 C、(a-b)(-a+b) D、(-a-b)(-a+b)6. 如表列出了一项实验的统计数据:
y
50
80
100
150
…
x
30
45
55
80
…
它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示变量y与x之间的关系式为( )
A、y=2x﹣10 B、y=x2 C、y=x+25 D、y=x+57. 下列式子正确的是( )A、(a﹣b)2=a2﹣2ab+b2 B、(a﹣b)2=a2﹣b2 C、(a﹣b)2=a2+2ab+b2 D、(a﹣b)2=a2﹣ab+b28. 如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( ) A、
A、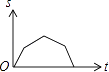 B、
B、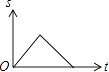 C、
C、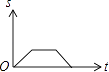 D、
D、 9. 若 则 的值为( )A、50 B、500 C、250 D、250010. 用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( )
9. 若 则 的值为( )A、50 B、500 C、250 D、250010. 用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( ) A、SSS B、SAS C、ASA D、AAS11. 如图,四边形ABCD与ECGF是两个边长分别为a , b的正方形,则阴影部分的面积可以表示为( )
A、SSS B、SAS C、ASA D、AAS11. 如图,四边形ABCD与ECGF是两个边长分别为a , b的正方形,则阴影部分的面积可以表示为( ) A、a2﹣ab+b2 B、 C、 D、a2+ab+b212. 如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P , 那么四边形PDCE的面积为( )
A、a2﹣ab+b2 B、 C、 D、a2+ab+b212. 如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P , 那么四边形PDCE的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算:a3•a3+(﹣2a3)2+(﹣a2)3= .14. 已知a、b、c是三角形的三边长,化简:|a﹣b+c|+|a﹣b﹣c|= .
15. 某市出租车的收费标准是:3千米以内(包括3千米)收费5元,超过3千米。每增加1千米加收1.2元,则路程x(x≥3)时,车费y(元)与路程x(千米)之间的关系式为:.16. 如图,等边△ABC边长为10,P在AB上,Q在BC延长线,CQ=PA , 过点P作PE⊥AC点E , 过点P作PF∥BQ , 交AC边于点F , 连接PQ交AC于点D , 则DE的长为 .
三、解答题
-
17. 计算:(1)、2﹣2+( )0+(﹣0.2)2014×52014(2)、(2a3b)3(﹣8ab2)÷(﹣4a4b3)(3)、(2a+1)2﹣(2a+1)(﹣1+2a)(4)、20192﹣2018×2020(运用整式乘法公式进行计算)18. 先化简,再求值:(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a= ,b= -1.19. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象回答:
 (1)、甲、乙两地之间的距离为;(2)、两车同时出发后h相遇;(3)、慢车的速度为千米/小时;快车的速度为千米/小时;(4)、线段CD表示的实际意义是 .20. 如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。
(1)、甲、乙两地之间的距离为;(2)、两车同时出发后h相遇;(3)、慢车的速度为千米/小时;快车的速度为千米/小时;(4)、线段CD表示的实际意义是 .20. 如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。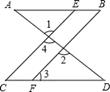
理由如下:
∵∠1 =∠2(已知),且∠1 =∠4( )
∴∠2 =∠4(等量代换)
∴CE∥BF( )
∴∠=∠3( )
又∵∠B =∠C(已知)
∴∠3 =∠B(等量代换)
∴AB∥CD( )
21. 如图,在△ABC中,CD⊥AB , 垂足为D , 点E在BC上,EF⊥AB , 垂足为F . (1)、CD与EF平行吗?为什么?(2)、如果∠1=∠2,且∠3=120°,求∠ACB的度数.22. 在△ABC中AB=AC , ∠BAC=90°,分别过
(1)、CD与EF平行吗?为什么?(2)、如果∠1=∠2,且∠3=120°,求∠ACB的度数.22. 在△ABC中AB=AC , ∠BAC=90°,分别过B、C作过A点的直线的垂线,垂足为
D、E .
 (1)、求证:△AEC≌△BDA;(2)、如果CE=2,BD=4,求ED的长是多少?23. 如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
(1)、求证:△AEC≌△BDA;(2)、如果CE=2,BD=4,求ED的长是多少?23. 如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒. (1)、试说明:AD∥BC;(2)、在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
(1)、试说明:AD∥BC;(2)、在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.