广东省中山市城东教学共进联盟2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期：2020-04-13 类型：期中考试
一、单选题
-
1. 下列二次根式中，属于最简二次根式的是（ ）
A、 B、 C、 D、2. 若 在实数范围内有意义，则x的取值范围是（ ）A、x＞0 B、x＞6 C、x≥6 D、x≤63. 以下列各组数为边长，能组成直角三角形的是（ ）A、1，1，2 B、2，3，4 C、2，2，2 D、2， ，4. 下列运算一定正确的是（ ）A、（a+b）2＝a2+b2 B、 ＝﹣3 C、a6÷a2＝a3 D、（a2）3＝a65. 下列命题的逆命题成立的是（ ）A、对顶角相等 B、全等三角形的对应角相等 C、如果两个数相等，那么它们的绝对值相等 D、两直线平行，同位角相等6. 已知一个直角三角形的两边长分别为3和4，则第三边长是（ ）A、5 B、25 C、 D、5或7. 下列说法正确的是（ ）A、对角线互相垂直的四边形是菱形 B、对角线相等的四边形是矩形 C、三条边相等的四边形是菱形 D、三个角是直角的四边形是矩形8. 如图所示：某商场有一段楼梯，高BC＝6m ， 斜边AC是10米，如果在楼梯上铺上地毯，那么需要地毯的长度是（ ）
A、8m B、10m C、14m D、24m9. 顺次连结菱形四边中点所得的四边形一定是（ ）A、平行四边形 B、矩形 C、菱形 D、正方形10. 如图，在矩形ABCD中，AB＝24，BC＝12，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（ ）
A、60 B、80 C、100 D、90二、填空题
-
11. 化简： ＝ ．12. 若|x﹣3|+ ＝0，则（ ）2018的值是 ．13. 如图，已知 ABCD中对角线AC，BD相交于点O，请你添加一个适当的条件，使 ABCD成为一个矩形．你添加的条件是 ．
14. 如图3，在▱ABCD中，AB＝5，AD＝8，DE平分∠ADC，则BE＝
15. 如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E是AC的中点．若DE=5，则AB的长为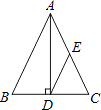
16.如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是 ．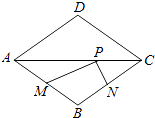
三、解答题
-
17. 计算：218. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：
(1)、在图①中画一条线段AB ， 使AB＝ ；(2)、在图②中画一个以格点为顶点，面积为2的正方形ABCD ．19. 如图，在▱ABCD中，已知点E、F在对角线边BD上，且BE＝DF ， 求证：四边形AECF是平行四边形．
20. 已知a＝ +2，b＝ ﹣2，求a2﹣b2的值．21. 如图，已知四边形ABCD中，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13，求四边形ABCD的面积.
22.已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．
23. 如图，点E是正方形ABCD对角线AC上一点，EF⊥AB ， EG⊥BC ， 垂足分别为E ， F ， 若正方形ABCD的周长是40cm ．
(1)、求证：四边形BFEG是矩形；(2)、求四边形EFBG的周长；(3)、当AF的长为多少时，四边形BFEG是正方形？24. 同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形，他沿矩形的对角线AC折出∠CAE＝∠DAC ， ∠ACF＝∠ACB的方法得到四边形AECF（如图）．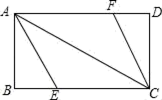
(1)、证明：四边形AECF是菱形；(2)、求菱形AECF的面积．25. 如图，在在四边形ABCD中，AD∥BC ， ∠B＝90°，且AD＝12cm ， AB＝8cm ， DC＝10cm ， 若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：
(1)、BC＝cm；(2)、当t＝秒时，四边形PQBA成为矩形．(3)、是否存在t ， 使得△DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由．