广东省佛山市南海区狮山镇2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-13 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $x < y$ ，则下列式子不成立的是（）

A、 $x - 1 < y - 1$ B、 $- 2 x < - 2 y$ C、 $x + 3 < y + 3$ D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称的是（）

A、 B、 C、 D、

查看试题解析
3. 一元一次不等式3(x+1)≤6的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
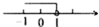4. 下列因式分解正确的是（）

A、12a²b﹣8ac+4a＝4a（3ab﹣2c） B、a²+ab+b²＝（a+b）² C、4b²+4b﹣1＝（2b﹣1）² D、﹣4x²+1＝（1+2x）（1﹣2x）

查看试题解析
5. 如图，一棵树在一次强台风中于离地面4米处折断倒下，倒下部分与地面成30°夹角，这棵树在折断前的高度为（）米．

A、4 B、8 C、12 D、 $3 + 3 \sqrt{3}$

查看试题解析
6. 已知多项式x²+bx+c因式分解的结果为（x﹣1）（x+2），则b+c的值为（）

A、﹣1 B、﹣2 C、2 D、0

查看试题解析
7. 如图，在△ABD中，AB的垂直平分线DE交BC于点D ， ∠B＝30°，AD＝AC ， ∠BAC的度数为（）

A、80° B、85° C、90° D、105°

查看试题解析
8. 若关于x的方程2x+2＝m﹣x的解为负数，则m的取值范围是（）

A、m＞2 B、m＜2 C、m＞ $\frac{2}{3}$ D、m＜ $\frac{2}{3}$

查看试题解析
9. 如图，在△ABC中，AB＝6，AC＝4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB，AC于M、N，则△AMN的周长为（）

A、12 B、10 C、8 D、不确定

查看试题解析
10. 已知：如图，在等边△ABC中取点P ，使得PA ， PB ， PC的长分别为3，4，5，将线段AP以点A为旋转中心顺时针旋转60°得到线段AD ，连接BD ，下列结论：
①△ABD可以由△APC绕点A顺时针旋转60°得到；②点P与点D的距离为3；③∠APB＝150°；

④S_△_APC+S_△_APB＝ $6 + \frac{9}{2} \sqrt{3}$ ，其中正确的结论有（）

A、①②④ B、①③④ C、①②③ D、②③④

查看试题解析

二、填空题

11. 分解因式： $2 a^{2} - 8 =$ ．

查看试题解析
12. 一个等腰三角形一边长为3cm，另一边长为7cm，那么这个等腰三角形的周长是cm.

查看试题解析
13.
如图是一次函数的y=kx+b图象，则关于x的不等式kx+b＞0的解集为

查看试题解析
14. 如图，点P是∠AOB的角平分线上一点，PD⊥OA于点D，CE垂直平分OP，若∠AOB=30°，OE=4，则PD= ．

查看试题解析
15. 两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝8，DH＝2，平移距离为3，则阴影部分的面积是．

查看试题解析
16. 如图，已知：∠MON＝30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，若OA₁＝1，则△A₇B₇A₈的边长为．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{matrix} \frac{1}{2} x + 2 \geq 0 \\ 1 - \frac{x + 5}{2} < - 1 - x \end{matrix}$ 并将解集在数轴上表示.

查看试题解析
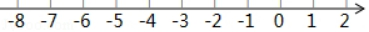18. 已知：x＝ $\sqrt{5}$ ，y＝ $\sqrt{5}$ ﹣2，求代数式x²﹣2xy+y²的值．

查看试题解析
19. 如图，在边长为1的正方形网格中，△ABC的顶点均在格点上，把△ABC绕点C逆时针旋转90°后得到△A₁B₁C．

(1)、画出△A₁B₁C，；

(2)、求在旋转过程中，CA所扫过的面积．

查看试题解析
20. 如图，在△ABC和△DCB中，∠A=∠D=90°，AC=BD，AC与BD相交于点O．

(1)、求证：△ABC≌△DCB；

(2)、△OBC是何种三角形？证明你的结论．

查看试题解析

21. 盐城市明达中学在一次爱心捐款活动中，全体同学积极踊跃捐款．现抽查了九年级（1）班全班同学捐款情况，并绘制出如下的统计表和统计图：

捐款（元）	20	50	100	150	200
人数（人）	4	12	9	3	2

求：

(1)、m＝， n＝；

(2)、求学生捐款数目的众数、中位数和平均数；

(3)、若该校有学生3500人，估计该校学生共捐款多少元？

查看试题解析

22. 快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣．已知购买甲型机器人1台，乙型机器人2台，共需14万元；购买甲型机器人2台，乙型机器人3台，共需24万元．

(1)、求甲、乙两种型号的机器人每台的价格各是多少万元；

(2)、已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件，该公司计划购买这两种型号的机器人共8台，总费用不超过41万元，并且使这8台机器人每小时分拣快递件数总和不少于8300件，则该公司有哪几种购买方案？哪个方案费用最低，最低费用是多少万元？

查看试题解析
23. “a²≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式.例如：x²+4x+5＝x²+4x+4+1＝（x+2）²+1，∵（x+2）²≥0，∴（x+2）²+1≥1，∴x²+4x+5≥1.试利用“配方法”解决下列问题：

(1)、填空：x²﹣4x+5＝（x）²+；

(2)、已知x²﹣4x+y²+2y+5＝0，求x+y的值；

(3)、比较代数式：x²﹣1与2x﹣3的大小.

查看试题解析
24.
如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．

(1)、如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证：AD=BE；
②求∠AEB的度数．

(2)、如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE中AE边上的高，试证明：AE=2 $\sqrt{3}$ CM+ $\frac{2 \sqrt{3}}{3}$ BN．

查看试题解析
25. 在平面直角坐标系xOy中，直线l₁：y＝ $\frac{1}{2}$ x+b与x轴交于点A，与y轴交于点B，且点C的坐标为（4，﹣4）．

(1)、点A的坐标为，点B的坐标为；（用含b的式子表示）

(2)、当b＝4时，如图所示．连接AC，BC，判断△ABC的形状，并证明你的结论；

(3)、过点C作平行于y轴的直线l₂ ，点P在直线l₂上．当﹣5＜b＜4时，在直线l₁平移的过程中，若存在点P使得△ABP是以AB为直角边的等腰直角三角形，请直接写出所有满足条件的点P的纵坐标．

查看试题解析