广东省番禺区六校教育教学联合体中段2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-13 类型：期中考试

进入出卷网下载

一、单选题

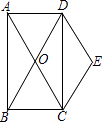
1. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{15}$ D、 $\frac{3}{\sqrt{2}}$

查看试题解析
2. 下列各组能组成直角三角形的是（）

A、4，5，6 B、2，3，4 C、11，12，13 D、8，15，17

查看试题解析
3. 下列四个式子中，x的取值范围为x≥2的是（　　）

A、 $\frac{\sqrt{x - 2}}{x - 2}$ B、 $\frac{1}{\sqrt{x - 2}}$ C、 $\sqrt{x - 2}$ D、 $\sqrt{2 - x}$

查看试题解析
4. 下列各式计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、2 $\sqrt{2}$ ﹣ $\sqrt{2}$ = $\sqrt{2}$ C、 $\sqrt{(- 4) \times (- 9)} = \sqrt{- 4} \times \sqrt{- 9}$ D、 $\sqrt{6}$ ÷ $\sqrt{3}$ = $\sqrt{3}$

查看试题解析
5. 下列结论中，错误的是（）

A、对角线互相垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、一组对边平行，一组对边相等的四边形是平行四边形 D、对角线互相垂直的四边形面积等于对角线乘积的一半

查看试题解析
6. 如图，矩形ABCD的两条对角线相交于点O，∠AOD=60°，AD=2，则AC的长是（）

A、2 B、4 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7.
如图，在平行四边形ABCD中，下列结论中错误的是（　　）

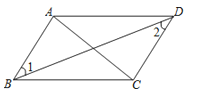A、∠1=∠2 B、∠BAD=∠BCD C、AB=CD D、AC⊥BD

查看试题解析
8. 直角三角形的两条直角边长为3和4，则该直角三角形斜边上的高为（）

A、5 B、7 C、 $\frac{12}{5}$ D、 $\frac{24}{5}$

查看试题解析
9. 如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
10. 如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB＝10，EF＝2，那么AH等于（）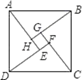

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

11. 命题“全等三角形的对应边都相等”的逆命题是命题．（填“真”或“假”）

查看试题解析
12. 如图，在▱ABCD中，已知∠D＝130°，则∠B＝度．

查看试题解析
13. 直角△ABC中，∠BAC =90°，D、E、F分别为AB、BC、AC的中点，已知DF=3，则AE= .

查看试题解析
14. 如图，数轴上点A表示的数为 $a$ ，化简： $a + \sqrt{a^{2} - 4 a + 4}$ = ．

查看试题解析
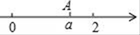15. 如图，已知圆柱的底面周长18cm ，高为12cm ，蚂蚁从A点爬到B点的最短路程是cm ．

查看试题解析
16. 在矩形ABCD中，AB=16，BC=8，将矩形沿其对角线AC折叠，点D落在点E处，且CE交AB于点F，则AF= ．

查看试题解析

三、解答题

17. 化简

(1)、 $\frac{\sqrt{48}}{\sqrt{6}}$ ；

(2)、 $\frac{3 \sqrt{a b^{3}}}{2 \sqrt{a b^{2}}}$ ；

(3)、6 $\sqrt{\frac{1}{3}}$ ；

查看试题解析
18. 计算

(1)、 $2 \sqrt{18} - 6 \sqrt{32} + \sqrt{2}$ ；

(2)、 $(2 \sqrt{48} - 3 \sqrt{27}) \div \sqrt{6}$

查看试题解析
19. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点．

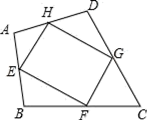
(1)、在图①中，以格点为端点，画线段MN＝ $\sqrt{17}$ ；

(2)、在图②中，以格点为顶点，画正方形ABCD ，使它的面积为13．

查看试题解析
20. 如图，四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点.
求证：四边形EFGH是平行四边形.

查看试题解析
21. 如图，在△ABC中，BD⊥AC ， AB＝20，BC＝15，CD＝9．

(1)、求AC的长；

(2)、判断△ABC的形状并证明．

查看试题解析
22.
如图，▱ABCD的对角线AC、BD相交于点O，AE=CF．

(1)、求证：△BOE≌△DOF；

(2)、若BD=EF，连接DE、BF，判断四边形EBFD的形状，无需说明理由.

查看试题解析
23. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．

(1)、求证：四边形OCED是菱形；

(2)、若∠BAC=30°，AC=4，求菱形OCED的面积．

查看试题解析
24. 如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF。

(1)、求证：△EBF≌△DFC；

(2)、求证：四边形AEFD是平行四边形；

(3)、①△ABC满足时，四边形AEFD是菱形。（无需证明）
②△ABC满足时，四边形AEFD是矩形。（无需证明）

③△ABC满足时，四边形AEFD是正方形。（无需证明）

查看试题解析