浙江台州市温岭三中2020年数学中考一模试卷

试卷更新日期：2020-04-10 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分

1. 规定：（→3）表示向右移动3，记作+3，则（←2）表示向左移动2，记作（　　）

A、+2 B、﹣2 C、+ $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 每年的3月12日是我国的植树节，某学校在“爱护地球，绿化祖国”的活动中，组织了100名学生开展植树造林活动，其植树情况整理如上表，则这100名学生所植树的中位数为（）

植树棵数

4

5

6

7

9

人数

30

20

27

15

8

A、4 B、5 C、5.5 D、6

查看试题解析
3. 十年来，我国知识产权战略实施取得显著成就，全国著作权登记量已达到274.8万件.数据274.8万用科学记数法表示为（）

A、2.748×10² B、274.8×10⁴ C、2.748×10⁶ D、0.2748×10⁷

查看试题解析
4. 如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α＝135°，则∠β等于（）

A、45° B、60° C、75° D、85°

查看试题解析
5. 如图，AB为⊙O的切线，切点为A，连接AO、BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（　　）

A、54° B、36° C、32° D、27°

查看试题解析
6. 某市要筑一水坝，需要在规定天数内完成，如果由甲队去做，恰能如期完成；如果由乙队去做，需超过规定天数三天．现由甲、乙两队合作2天后，余下的工程由乙队独自做，恰好在规定天数内完成．设规定的天数为x，下面所列方程正确的是（　　）

A、 $\frac{2}{x} + \frac{x}{x + 3} = 1$ B、 $\frac{2}{x} = \frac{x}{x + 3}$ C、 $(\frac{1}{x} + \frac{x}{x + 3}) \times 2 + \frac{x}{x + 3} \cdot (x - 2) = 1$ D、 $(\frac{1}{x} + \frac{x}{x + 3}) = 1$

查看试题解析
7. 定义一种新运算 $\int_{b}^{a} n \cdot x^{n - 1} d x$ ＝aⁿ﹣bⁿ ，例如 $\int_{n}^{k} 2 x d x$ ＝k²﹣n² ，若 $\int_{m^{2} - 1}^{m - 1} - x^{- 2} d x$ ＝﹣ $\frac{1}{2}$ ，则m为（　　）

A、﹣1+ $\sqrt{2}$ B、﹣1﹣ $\sqrt{2}$ C、 $\sqrt{2}$ ±1 D、﹣1± $\sqrt{2}$

查看试题解析
8. 已知函数y₁＝ ${\begin{cases} - x - 1 (x \leq - 1) \\ x + 1 (- 1 < x \leq 0) \\ - x + 1 (0 < x \leq 1) \\ x - 1 (x > 1) \end{cases}$ 的图象为“W”型，直线y＝kx﹣k+1与函数y₁的图象有三个公共点，则k的值是（　　）

A、1或 $\frac{1}{2}$ B、0或 $\frac{1}{2}$ C、 $\frac{1}{2}$ D、 $\frac{1}{2}$ 或﹣ $\frac{1}{2}$

查看试题解析
9. 如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P，M．对于下列结论：①△BAE∽△CAD；②AP⊥CD；③AC²＝CP•CM．其中正确的是（　　）

A、①②③ B、①② C、①③ D、②③

查看试题解析
10. 如图，在菱形ABCD中，∠A＝60°，AD＝4，点F是AB的中点，过点F作FE⊥AD，垂足为E，将△AEF沿点A到点B的方向平移，得到△A'E'F'，设点P、P'分别是EF、E'F'的中点，当点A'与点B重合时，四边形PP'CD的面积为（）

A、7 $\sqrt{3}$ B、6 $\sqrt{3}$ C、8 $\sqrt{3}$ D、8 $\sqrt{3}$ ﹣4

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

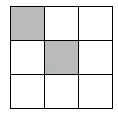
11. 当x时， $\sqrt{\frac{- 1}{x - 1}}$ 有意义．

查看试题解析
12. 已知a﹣2＝b+c，则代数式a（a﹣b﹣c）﹣b（a﹣b﹣c）﹣c（a﹣b﹣c）的值等于．

查看试题解析
13. 如图，把大正方形平均分成9个小正方形，其中有2个小正方形已被涂黑，在剩余的7个白色小正方形中任选一个也涂黑，则使整个涂黑部分成为轴对称图形的概率是．

查看试题解析
14. 七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”．由边长为4 $\sqrt{2}$ 的正方形ABCD可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型（其中点Q、R分别与图2中的点E、G重合，点P在边EH上），则“拼搏兔”所在正方形EFGH的边长是．

查看试题解析
15. 在半径为2的⊙O中，弦AB＝2 $\sqrt{2}$ ，连接OA，OB．在直线OB上取一点K，使tan∠BAK＝ $\frac{1}{2}$ ，则△OAK的面积为．

查看试题解析
16. 如图，已知△ABC，△DEF均为等腰直角三角形，EF＝10 $\sqrt{2}$ ，顶点D，E分别在边AB，AC上滑动.则在滑动过程中，点A，F间距离的最大值为.

查看试题解析

三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）

17.

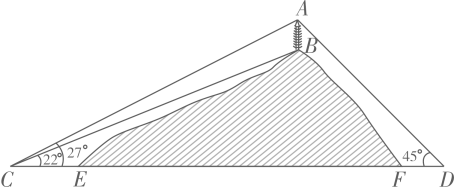
(1)、计算： $\sqrt{9}$ ﹣|2﹣ $\sqrt{2}$ |﹣（π﹣3.14）⁰+（﹣1）²⁰²⁰

(2)、先化简，再求值： $\frac{a^{2} - 3 a}{a + 2}$ ÷（a﹣2﹣ $\frac{5}{a + 2}$ ）+ $\frac{a^{2} - a}{a + 3}$ ，其中a²﹣2a﹣6＝0

查看试题解析
18. 解不等式组 ${\begin{cases} 4 (x + 1) \leq 7 x + 13 \\ x - 4 < \frac{x - 8}{3} \end{cases}$ ，并写出它的所有负整数解

查看试题解析
19. 如图，山顶有一塔AB，塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°，从与F点相距50m的D处测得A的仰角为45°.求隧道EF的长度.（参考数据：tan22°≈0.40，tan27°≈0.51）

查看试题解析
20. 如图，在矩形ABCD中，AB＝2，AD＝4．点E，F分别在AD，BC上，点A与点C关于EF所在的直线对称，P是边DC上的一动点．

(1)、连接AF，CE，求证：四边形AFCE是菱形；

(2)、当△PEF的周长最小时，求 $\frac{D P}{C P}$ 的值．

查看试题解析
21. 酒令是中国民间风俗之一．白居易曾诗曰：“花时同醉破春愁，醉折花枝当酒筹”饮酒行令，是中国人在饮酒时助兴的一种特有方式，不仅要以酒助兴，往往还伴之以赋诗填词、猜迷形拳之举，最早诞生于西周，完备于隋唐，“虎棒鸡虫令”是其中一种：“二人相对，以筷子相声，同时或喊虎、喊棒、喊鸡、喊虫，以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负，负者饮．若棒兴鸡、或虫兴虎同时出现（解释：若棒与鸡，虎与虫同时喊出）或两人喊出同一物，则不分胜负，继续喊”．依据上述规则，张三和李四同时随机地喊出其中一物，两人只喊一次．

(1)、求张三喊出“虎”取胜的概率；

(2)、用列表法或画树状图法，求李四取胜的概率；

(3)、直接写出两人能分出胜负的概率．

查看试题解析
22. 如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．

(1)、求证：直线DF是⊙O的切线；

(2)、求证：BC²＝4CF•AC；

(3)、若⊙O的半径为4，∠CDF＝15°，求阴影部分的面积．

查看试题解析
23. 抛物线 $y = a x^{2} - \frac{1}{2} x + \frac{5}{4}$ 经过点E（5，5），其顶点为C点．

(1)、求抛物线的解析式，并直接写出C点坐标．

(2)、将直线 $y = \frac{1}{2} x$ 沿y轴向上平移b个单位长度交抛物线于A、B两点．若∠ACB＝90°，求b的值．

(3)、是否存在点D（1，a），使抛物线上任意一点P到x轴的距离等于P点到点D的距离？若存在，请求点D的坐标；若不存在，请说明理由．

查看试题解析
24. 在平面直角坐标系xOy中，有不重合的两个点Q（x₁ ， y₁）与P（x₂ ， y₂）．若Q，P为某个直角三角形的两个锐角顶点，且该直角三角形的直角边均与x轴或y轴平行（或重合），则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“折距”，记做D_PQ ．特别地，当PQ与某条坐标轴平行（或重合）时，线段PQ的长即点Q与点P之间的“折距”．例如，在图1中，点P（1，﹣1），点Q（3，﹣2），此时点Q与点P之间的“折距”D_PQ＝3．

(1)、①已知O为坐标原点，点A（3，﹣2），B（﹣1，0），则D_AO＝　▲ ， D_BO＝▲ ．
②点C在直线y＝﹣x+4上，请你求出D_CO的最小值．

(2)、点E是以原点O为圆心，1为半径的圆上的一个动点，点F是直线y＝3x+6上以动点．请你直接写出点E与点F之间“折距”D_EF的最小值．

查看试题解析

植树棵数	4	5	6	7	9
人数	30	20	27	15	8