河北省遵化市2020年中考数学二模考试试卷
试卷更新日期:2020-04-09 类型:中考模拟
一、选择题(本大题共16个小题,共42分,1~10小题,每小题3分;11~16小题,每小题2分。)
-
1. - =( )A、3 B、 C、 D、2. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、113.
用八根木条钉成如图所示的八边形木架,要使它不变形,至少要钉上木条的根数是( )
 A、3根 B、4根 C、5根 D、6根4. 由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A、3根 B、4根 C、5根 D、6根4. 由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )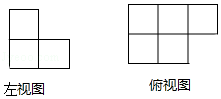 A、5 B、6 C、7 D、85. 55万用科学记数法表示为( )A、5.5×106 B、5.5×105 C、5.5×104 D、5.5×1036. 关于 的叙述正确的是( )A、 B、在数轴上不存在表示 的点 C、 =±2 D、与 最接近的整数是37. 如表是某公司员工月收入的资料.
A、5 B、6 C、7 D、85. 55万用科学记数法表示为( )A、5.5×106 B、5.5×105 C、5.5×104 D、5.5×1036. 关于 的叙述正确的是( )A、 B、在数轴上不存在表示 的点 C、 =±2 D、与 最接近的整数是37. 如表是某公司员工月收入的资料.月收入/元
45000
18000
10000
5500
5000
3400
3300
1000
人数
1
1
1
3
6
1
11
1
能够反映该公司全体员工月收入水平的统计量是( )
A、平均数和众数 B、平均数和中位数 C、中位数和众数 D、平均数和方差8. 如图,三角形纸片 , ,点E为AB的中点.沿过点E的直线折叠,使点B与点A重合,折痕EF交BC于点F.已知 ,则BC的长是( )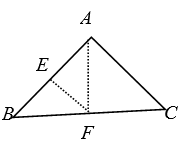 A、 B、 C、3 D、9. 已知: , 则 的值是( )A、 B、 C、3 D、-310. 如图在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A、 B、 C、3 D、9. 已知: , 则 的值是( )A、 B、 C、3 D、-310. 如图在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )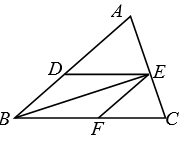 A、AB=AC B、AD=BD C、BE⊥AC D、BE平分∠ABC11. 若 ,则x,y的值为( )A、 B、 C、 D、12. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A、AB=AC B、AD=BD C、BE⊥AC D、BE平分∠ABC11. 若 ,则x,y的值为( )A、 B、 C、 D、12. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )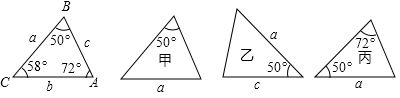 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙13. 已知a , b是有理数,则a2 -2a+4的最小值是( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙13. 已知a , b是有理数,则a2 -2a+4的最小值是( )
A、3 B、5 C、6 D、814. 已知二次函数y=-x2-4x-5,左、右平移该抛物线,顶点恰好落在正比例函数y=-x的图象上,则平移后的抛物线的解析式为( )A、y=-x2-4x-1 B、y=-x2-4x-2 C、y=-x2+2x-1 D、y=-x2+2x-215. 如图3,在5×5正方形网格中,一条圆弧经过A , B , C三点,那么这条圆弧所在圆的圆心是( ) A、点P B、点R C、点Q D、点M16. 如图,在 中, 平分 交 于点 ,过点 作 交 于点 ,且
A、点P B、点R C、点Q D、点M16. 如图,在 中, 平分 交 于点 ,过点 作 交 于点 ,且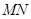 平分 ,若 ,则 的长为( )
平分 ,若 ,则 的长为( )  A、
A、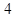 B、
C、
D、
B、
C、
D、
二、填空题 (本大题有3个小题,共12分,17~18小题各3分;19小题有2个空,每空3分。)
-
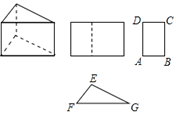
17. 已知a与b的和为2,b与c互为相反数,若 =1,则a=.18. 三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为cm.
 19. 阅读下文,寻找规律填空:
19. 阅读下文,寻找规律填空:已知x≠1时,(1-x)(1+x)=1-x2 , (1-x)(1+x+x2)=1-x3 , (1-x)(1+x+x2+x3)=1-x4…
(1)、(1-x)()=1-x8;(2)、观察上式,并猜想:(1-x)(1+x+x2+…+xn)= .三、解答题(本大题有7个小题,共66分。)
-
20. 利用平方差公式可以进行简便计算:
例1:99×101=(100-1)(100+1)=1002-12=10 000-1=9 999;
例2:39×410=39×41×10=(40-1)(40+1)×10=(402-12)×10=(1600-1)×10=1599×10=15 990.
请你参考上述算法,运用平方差公式简便计算:
(1)、 ;(2)、(2 019 +2 019 )( - ).21. 如图,E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F. (1)、求证:△ADE≌△FCE.(2)、若∠BAF=90°,BC=5,EF=3,求平行四边形ABCD的面积.22. 为了发展学生的核心素养,培养学生的综合能力,石家庄某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)
(1)、求证:△ADE≌△FCE.(2)、若∠BAF=90°,BC=5,EF=3,求平行四边形ABCD的面积.22. 为了发展学生的核心素养,培养学生的综合能力,石家庄某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)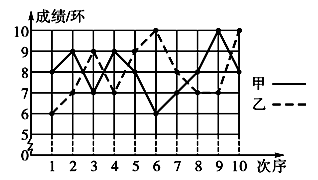 (1)、依据折线统计图,得到下面的表格:
(1)、依据折线统计图,得到下面的表格:射击次序(次)
1
2
3
4
5
6
7
8
9
10
甲的成绩(环)
8
9
7
9
8
6
7

10
8
乙的成绩(环)
6
7
9
7
9
10
8
7
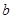
10
其中
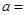 ,
, 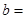 ;(2)、甲成绩的众数是环,乙成绩的中位数是环;(3)、请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?(4)、该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.23. 机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°= ,cos67.4°= ,tan67.4°= )
;(2)、甲成绩的众数是环,乙成绩的中位数是环;(3)、请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?(4)、该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.23. 机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°= ,cos67.4°= ,tan67.4°= ) (1)、求弦BC的长;(2)、请判断点A和圆的位置关系,试说明理由.24. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为 (单位:km),乘坐地铁的时间 (单位:min)是关于 的一次函数,其关系如下表:
(1)、求弦BC的长;(2)、请判断点A和圆的位置关系,试说明理由.24. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为 (单位:km),乘坐地铁的时间 (单位:min)是关于 的一次函数,其关系如下表:地铁站
A
B
C
D
E
x/km
7
9
11
12
13
y1/min
16
20
24
26
28
(1)、求 关于 的函数解析式;(2)、李华骑单车的时间 (单位:min)也受 的影响,其关系可以用 = 2-11 +78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最短时间.25. 已知Rt△OAB , ∠OAB=90o , ∠ABO=30o , 斜边OB=4,将Rt△OAB绕点O顺时针旋转60o , 如图1,连接BC. (1)、ΔOBC的形状是;(2)、如图1,连接AC , 作OP⊥AC , 垂足为P , 求OP的长度;(3)、如图2,点M、N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒.设运动时间为x秒,△OMN的面积为y , 求当x为何值时y取得最大值?最大值为多少?(结果可保留根号)26. 如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c .
(1)、ΔOBC的形状是;(2)、如图1,连接AC , 作OP⊥AC , 垂足为P , 求OP的长度;(3)、如图2,点M、N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒.设运动时间为x秒,△OMN的面积为y , 求当x为何值时y取得最大值?最大值为多少?(结果可保留根号)26. 如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c .阅读理解:
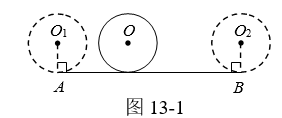
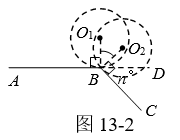
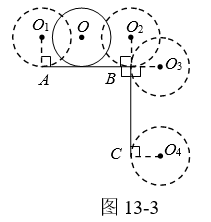


①如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c时,⊙O恰好自转1周.
②如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的角∠O1BO2 = n°,⊙O在点B处自转 周.
(1)、实践应用:在阅读理解的①中,若AB = 2c , 则⊙O自转周;若AB=1 , 则⊙O自转周.在阅读理解的②中,若∠ABC = 120°,则⊙O在点B处自转周;若∠ABC = 60°,则⊙O在点B处自转周.
(2)、如图13-3,∠ABC=90°,AB=BC= c . ⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转周.(3)、拓展联想:如图13-4,△ABC的周长为l , ⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
(4)、如图13-5,多边形的周长为l , ⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.