河北省石家庄42中2020年中考数学二模考试试卷
试卷更新日期:2020-04-09 类型:中考模拟
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.)
-
1. 一种零件的直径尺寸在图纸上是 (单位:mm),它表示这种零件的标准尺寸是20mm , 则加工要求尺寸最大不超过( )A、0.03mm B、0.02nn C、20.03mm D、19.98mm2. 将一副三角板按如图所示位置摆放,其中∠α=∠β的是( )
 A、①② B、②③ C、①④ D、②④3. 在数轴上与原点的距离小于8的点对应的x满足( )A、﹣8<x<8 B、x<﹣8或x>8 C、x<8 D、x>84. 北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,遇极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道AB在点O南偏东70°的方向上,则这条跑道所在射线OB与正北方向所成角的度数为( )
A、①② B、②③ C、①④ D、②④3. 在数轴上与原点的距离小于8的点对应的x满足( )A、﹣8<x<8 B、x<﹣8或x>8 C、x<8 D、x>84. 北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,遇极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道AB在点O南偏东70°的方向上,则这条跑道所在射线OB与正北方向所成角的度数为( )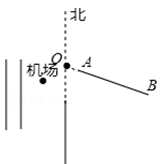 A、20° B、70° C、110° D、160°5. 在下列图形中是轴对称图形的是( )A、
A、20° B、70° C、110° D、160°5. 在下列图形中是轴对称图形的是( )A、 B、
B、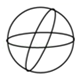 C、
C、 D、
D、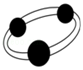 6. 下列事件中,属于不可能事件的是( )A、某个数的绝对值大于0 B、任意一个五边形的外角和等于540° C、某个数的相反数等于它本身 D、长分别为3,4,6的三条线段能围成一个三角形7. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、
6. 下列事件中,属于不可能事件的是( )A、某个数的绝对值大于0 B、任意一个五边形的外角和等于540° C、某个数的相反数等于它本身 D、长分别为3,4,6的三条线段能围成一个三角形7. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、 B、
B、 C、
C、 D、
D、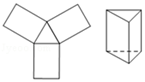 8. 已知△ABC , 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB , AC上,且这组对应边所对的顶点重合于点M , 点M一定在( )
8. 已知△ABC , 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB , AC上,且这组对应边所对的顶点重合于点M , 点M一定在( )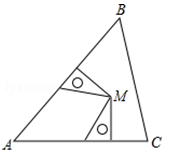 A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上9. 如图,在菱形ABCD中,E是AB的中点,F点是AC的中点,连接EF . 如果EF=4,那么菱形ABCD的周长为( )
A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上9. 如图,在菱形ABCD中,E是AB的中点,F点是AC的中点,连接EF . 如果EF=4,那么菱形ABCD的周长为( ) A、9 B、12 C、24 D、3210. 若关于x的一元二次方程nx2﹣2x﹣1=0无实数根,则一次函数y=(n+1)x﹣n的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 如图,已知∠MON及其边上一点A . 以点A为圆心,AO长为半径画弧,分别交OM , ON于点B和C . 再以点C为圆心,AC长为半径画弧,恰好经过点B . 错误的是( )
A、9 B、12 C、24 D、3210. 若关于x的一元二次方程nx2﹣2x﹣1=0无实数根,则一次函数y=(n+1)x﹣n的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 如图,已知∠MON及其边上一点A . 以点A为圆心,AO长为半径画弧,分别交OM , ON于点B和C . 再以点C为圆心,AC长为半径画弧,恰好经过点B . 错误的是( )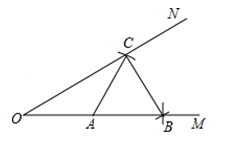 A、S△AOC=S△ABC B、∠OCB=90° C、∠MON=30° D、OC=2BC12. 两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部需x个月,则根据题意可列方程中错误的是( )A、 + =1 B、 + + =1 C、 + =1 D、 +2( + )=113. 如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
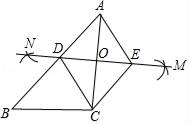
A、S△AOC=S△ABC B、∠OCB=90° C、∠MON=30° D、OC=2BC12. 两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部需x个月,则根据题意可列方程中错误的是( )A、 + =1 B、 + + =1 C、 + =1 D、 +2( + )=113. 如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:①分别以A、C为圆心,以大于 AC的长为半径在AC两边作弧,交于两点M、N;②连接MN,分别交AB、AC于点D、O;③过C作CE∥AB交MN于点E,连接AE、CD.则四边形ADCE的周长为( )
 A、10 B、20 C、12 D、2414. 下图中反比例函数y= 与一次函数y=kx﹣k在同一直角坐标系中的大致图象是( )A、
A、10 B、20 C、12 D、2414. 下图中反比例函数y= 与一次函数y=kx﹣k在同一直角坐标系中的大致图象是( )A、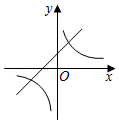 B、
B、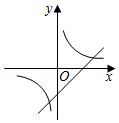 C、
C、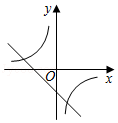 D、
D、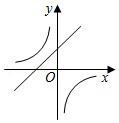 15. 有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机地放入其中两个信封里,则信封与信编号都相同的概率为( )A、 B、 C、 D、16. 如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P , 点B与点O重合,且AC大于OE , 将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x , 则x的取值范围是( )
15. 有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机地放入其中两个信封里,则信封与信编号都相同的概率为( )A、 B、 C、 D、16. 如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P , 点B与点O重合,且AC大于OE , 将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x , 则x的取值范围是( )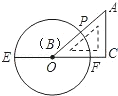 A、30≤x≤60 B、30≤x≤90 C、30≤x≤120 D、60≤x≤120
A、30≤x≤60 B、30≤x≤90 C、30≤x≤120 D、60≤x≤120二、填空题
-
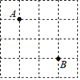
17. 如图,边长为1的正方形网格中,AB3.(填“>”,“=”或“<”)
 18. 若 ,则 = .19. 已知:如图,在平面直角坐标系xOy中,点A在抛物线y=x2﹣4x+6上运动,
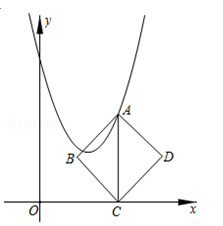
18. 若 ,则 = .19. 已知:如图,在平面直角坐标系xOy中,点A在抛物线y=x2﹣4x+6上运动,过点A作AC⊥x轴于点C , 以AC为对角线作正方形ABCD。
则抛物线y=x2﹣4x+6的顶点是是 .
正方形的边长AB的最小值是 .
三、解答题(本大题共6个小题,共68分.)
-
20.(1)、计算2 ﹣3 ﹣5 +(﹣3 )(2)、某同学做一道数学题:“两个多项式A、B , B=3x2﹣2x﹣6,试求A+B”,这位同学把“A+B”看成“A﹣B”,结果求出答案是﹣8x2+7x+10,那么A+B的正确答案是多少?21. 如图
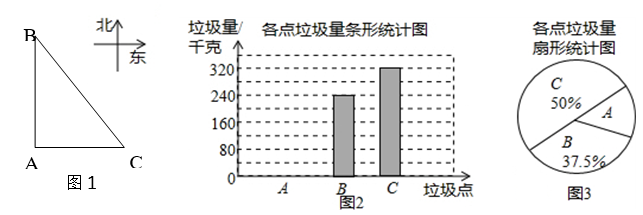
如图1,A , B , C是郑州市二七区三个垃圾存放点,点B , C分别位于点A的正北和正东方向,AC=40米.八位环卫工人分别测得的BC长度如下表:
甲
乙
丙
丁
戊
戌
申
辰
BC(单位:米)
84
76
78
82
70
84
86
80
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
(1)、表中的中位数是、众数是;(2)、求表中BC长度的平均数(3)、求A处的垃圾量,并将图2补充完整;(4)、用(1)中的 作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.22. 已知:在Rt△ABC中,∠ACB=90°,AC=BC , D是线段AB上一点,连结CD , 将线段CD绕点C逆时针旋转90°得到线段CE , 连结DE , BE . (1)、依题意补全图形;(2)、若∠ACD=α,用含α的代数式表示∠DEB .(3)、若△ACD的外心在三角形的内部,请直接写出α的取值范围.23. 如图,在平面直角坐标系中,点O为坐标原点,点A(0,3)与点B关于x轴对称,点C(n , 0)为x轴的正半轴上一动点.以AC为边作等腰直角三角形ACD , ∠ACD=90°,点D在第一象限内.连接BD , 交x轴于点F .
(1)、依题意补全图形;(2)、若∠ACD=α,用含α的代数式表示∠DEB .(3)、若△ACD的外心在三角形的内部,请直接写出α的取值范围.23. 如图,在平面直角坐标系中,点O为坐标原点,点A(0,3)与点B关于x轴对称,点C(n , 0)为x轴的正半轴上一动点.以AC为边作等腰直角三角形ACD , ∠ACD=90°,点D在第一象限内.连接BD , 交x轴于点F .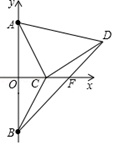 (1)、如果∠OAC=38°,求∠DCF的度数;(2)、直接写出用含n的式子表示点D的坐标;(3)、在点C运动的过程中,判断OF的长是否发生变化?若不变求出其值,
(1)、如果∠OAC=38°,求∠DCF的度数;(2)、直接写出用含n的式子表示点D的坐标;(3)、在点C运动的过程中,判断OF的长是否发生变化?若不变求出其值,若变化请说明理由.
24. 有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以am/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题: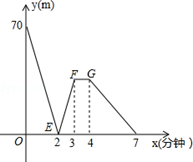 (1)、A、B两点之间的距离是m , A、C两点之间的距离是m , a=m/min:(2)、求线段EF所在直线的函数表达式?(3)、设线段FG∥x轴.
(1)、A、B两点之间的距离是m , A、C两点之间的距离是m , a=m/min:(2)、求线段EF所在直线的函数表达式?(3)、设线段FG∥x轴.①当3≤x≤4时,甲机器人的速度为m/min .
25. 如图,在△AOB中,∠AOB=90°,AO=6,BO=6 ,以点O为圆心,以2为半径作优弧 ,交AO于点D , 交BO于点E . 点M在优弧 上从点D开始移动,到达点E时停止,连接AM .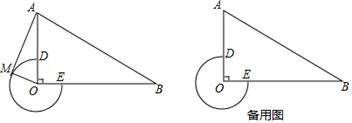 (1)、当AM=4 时,判断AM与优弧 的位置关系,并加以证明;(2)、当MO∥AB时,求点M在优弧 上移动的路线长及线段AM的长;(3)、连接BM , 设△ABM的面积为S , 直接写出S的取值范围.26. 如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B , 与y轴交于点C , 且OC=2OB , 点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH , 点H、F在抛物线上,点E在x轴上.
(1)、当AM=4 时,判断AM与优弧 的位置关系,并加以证明;(2)、当MO∥AB时,求点M在优弧 上移动的路线长及线段AM的长;(3)、连接BM , 设△ABM的面积为S , 直接写出S的取值范围.26. 如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B , 与y轴交于点C , 且OC=2OB , 点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH , 点H、F在抛物线上,点E在x轴上.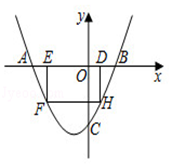 (1)、求抛物线的解析式;(2)、当矩形DEFH的周长最大时,求矩形DEFH的面积;(3)、在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N , 连接M、N . 若MN恰好平分矩形DEFH的面积,求m的值.
(1)、求抛物线的解析式;(2)、当矩形DEFH的周长最大时,求矩形DEFH的面积;(3)、在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N , 连接M、N . 若MN恰好平分矩形DEFH的面积,求m的值.