江苏省镇江市2019-2020学年八年级下学期数学3月月考试卷B卷
试卷更新日期：2020-04-08 类型：月考试卷
一、填空题（本大题共有12小题，每小题3分，共计36分．）
-
1. 对1850个数据进行整理．在频数的统计表中，各组的频率之和等于.2. 至少需要调查名同学，才能使“有两个同学的生日在同一天”这个事件为必然事件．3. 为了帮助残疾人，某地举办“即开型"福利彩票销售活动，规定每10万张为一组，其中有10名一等奖，100名二等奖，1 000名三等奖，5 000名爱心奖，小明买了10张彩票，则他中奖的概率为.4. 在样本容量为200的频数直方图中，共有3个小长方形，若第一个长方形对应的频率为10%，若中间一个小长方形的高与其余两个小长方形高的和之比是2：3，则中间一组的频率为.5. 矩形的一个内角平分线把矩形一条边分成3 cm和5 cm两部分，则矩形的周长为.
6. 如图，▱ABCD与▱DCFE的周长相等，且∠BAD＝60°，∠DAE＝25°，则∠F的度数为。
7. 四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于点H，则DH=.8. 如图，在平行四边形ABDC中， 是由 绕顶点 旋转40°所得，顶点 恰好转到 上一点 的位置，则 =度.
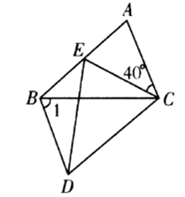9. 如图，点E是矩形纸片ABCD的边AB的中点，点G是BC上的一点，∠BEG﹥60⁰，现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等（不包含∠BEG）的角有个.
10. 如图，矩形ABCD的面积为20 cm2 ， 对角线交于点O，以AB、AO为邻边作平行四边形 AOC1B ，对角线交于点O1；以AB、A O1 为邻边作平行四边形 AO1C1B ▪▪▪▪▪▪，依此类推，则平行四边形 AO3C4B 的面积为.
11. 如图，正方形 ABCD 的边长为2， △ABE是等边三角形，点 E在正方形 ABCD 内，在对角线 AC 上有一点 P ，使 PD+PE 的和最小，则这个最小值为.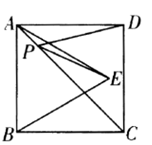
12. 如图，△ACE是以▱ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称，CE交x轴于点H，若E点的坐标是（7， ），则D点的坐标是 ．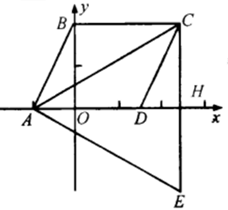
二、选择题（本大题共有6小题，每小题3分，共计18分．在每小题所给出的四个选项中，恰有一项符合题目要求．）
-
13. 甲、乙两位同学在一次实验中统计了某一结果出现的频率，给出的统计图如图所示，则符合这一结果的实验可能是（ ）
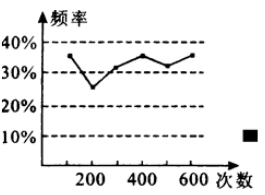A、掷一枚正六面体的骰子，出现5点的概率 B、掷一枚硬币，出现正面朝上的概率 C、任意写出一个整数，能被2整除的概率 D、一个袋子中装着只有颜色不同，其他都相同的 两个红球和一个黄球，从中任意取出一个是黄球的概率14. 一个不透明的袋子中装有2个红球、3个白球，每个球除颜色外都相同．从中任意摸出3个球，下列事件为必然事件的是（ ）A、至少有1个球是红球 B、有1个球是白球 C、至少有2个球是红球 D、至少有2个球是白球15. 下列图形：①等腰三角形；②平行四边形；③矩形；④菱形；⑤正方形．用两个全等但不是等腰的直角三角形，一定能拼成的是（ ）A、①②③ B、②③④ C、①③⑤ D、①②③④⑤16. 如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是（ ）
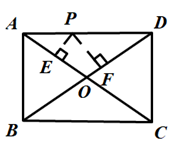A、 B、 C、 D、无法确定17. 如图，点E、F分别是菱形ABCD的边 AD、DC的中点，如果阴影部分的面积和是10，则菱形对角线AC与BD的乘积 等于（ ）
A、10 B、32 C、20 D、1618. 小明尝试着将矩形纸片 ABCD （如图（1） ，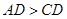
）沿过点 A 的直线折叠，使得点 B 落在边 AD 上的点 F 处，折痕为 AE ，如图（2），再沿过点 D 的直线折叠，使得点 C 落在边 DA 上的点 N 处，点 E 落在边 AE 上的点 M 处，折痕为 DG ，如图（3），如果第二次折叠后，点 M 正好在 ∠NDG 的平分线上，那么矩形ABCD长与宽的比值为（ ）
A、
B、
C、
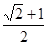D、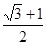
三、解答题（本大题共有4小题,共计46分．解答时应写出必要的文字说明、证明过程或演算步骤．）
-
19. 近几年某市加大中职教育投入力度，取得了良好的社会效果．某校随机调查了九年级m名学生的升学意向，并根据调查结果绘制出不完整的统计表如下：
升学意向
省级示范高中
市级示范高中
其他普高
职业高中
其他
合计
人数
15
15
9
3
m
百分比
25%
25%
n
5%
100%
请你根据统计表提供的信息解答下列问题：
(1)、表中m的值为 ， n的值为；(2)、补全条形统计图；(3)、若该校九年级有学生500名，估计该校大约有多少名毕业生的升学意向是职业高中？20. 小强和小明两个同学设计一种同时向上抛出1元硬币的游戏，游戏规则如下：如果抛出的硬币落下后朝上的两个面都为1元，则小强得1分，其余情况小明得1分，谁先得到10分谁就赢得比赛.你认为这个游戏规则公平吗?若不公平，怎样改正?21.如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．
(1)、求证：四边形AECF是平行四边形；(2)、若AB=6，AC=10，求四边形AECF的面积．22. 如图，在▱ABCD中，AB⊥AC，对角线BD、AC交于点O．将直线AC绕点O顺时针旋转分别交BC、AD于点E、F．
(1)、试说明在旋转过程中，AF与CE总保持相等；(2)、把旋转角∠AOF记作α，当α等于多少时，四边形ABEF是平行四边形，请说明理由；(3)、在旋转过程中，四边形AECF可能是矩形吗?如果不能，请说明理由；如果能，说明此时旋转角α与∠ABC之间的关系.