江苏省镇江市2019-2020学年八年级下学期数学3月月考试卷A卷
试卷更新日期:2020-04-08 类型:月考试卷
一、填空题(本大题共有12小题,每小题3分,共计36分.)
-
1. 为了解市中小学生对春节联欢晚会语言类节目喜爱的程度,这项调查采用方式调査较好.(填“普查”或“抽样调查”)2. 某中学数学教研组有25名教师,将他们按年龄分组,在38~45岁组内的教师有8名教师,那么这个小组的频率是.3. “同位角相等”是事件.(填“确定”或“随机”)4. 在一个不透明的袋中,装有3个红球和2个白球,这些球除颜色外其余都相同,搅匀后从中随机摸出一个球,这个球是红球的可能性是.5. 如图中的图形绕着中心至少旋转度能与自身重合.
 6. 如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为.
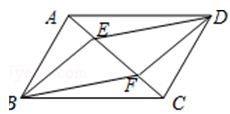
6. 如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为.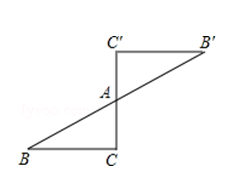 7. 如图,平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为.
7. 如图,平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为.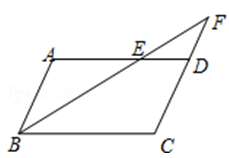 8. 如图,平行四边形ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
8. 如图,平行四边形ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .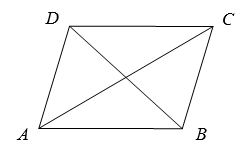 9. 已知一个菱形的周长是20 cm,两条对角线的比是4:3,则这个菱形的面积是 .10. 已知:如图,矩形ABCD的长和宽分别为2和1,以D为圆心,AD为半径作AE弧,再以AB的中点F为圆心,FB长为半径作BE弧,则阴影部分的面积为 .
9. 已知一个菱形的周长是20 cm,两条对角线的比是4:3,则这个菱形的面积是 .10. 已知:如图,矩形ABCD的长和宽分别为2和1,以D为圆心,AD为半径作AE弧,再以AB的中点F为圆心,FB长为半径作BE弧,则阴影部分的面积为 .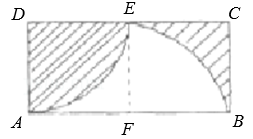 11. 工人师博常常通过测量平行四边形零件的对角线是否相等来检验零件是否为矩形,请问工人师博此种检验方法依据的道理是.12. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快s后,四边形ABPQ成为矩形.
11. 工人师博常常通过测量平行四边形零件的对角线是否相等来检验零件是否为矩形,请问工人师博此种检验方法依据的道理是.12. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快s后,四边形ABPQ成为矩形.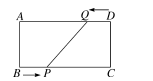
二、选择题(本大题共有6小题,每小题3分,共计18分.在每小题所给出的四个选项中,恰有一项符合题目要求.)
-
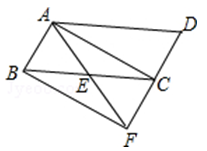
13. 完成下列任务,宜用抽样调查的是( )A、调查你班同学的年龄情况 B、了解你所在学校男、女生人数 C、考察一批炮弹的杀伤半径 D、奥运会上对参赛运动员进行的尿样检查14. 下列事件中,是随机事件的是( )A、画一个三角形,其内角和是180° B、在一只装了红色卡片的袋子里,摸出一张白色卡片 C、掷一枚正六面体骰子,朝上一面的点数小于7 D、在一副扑克牌中抽出一张,抽出的牌是黑桃615. 下列性质中,菱形具有而矩形不一定具有的是( )A、对角线互相平分 B、对角线互相垂直 C、对边平行且相等 D、对角线相等16. 如图,△ABC与△ 关于点O成中心对称,则下列结论不成立的是( )
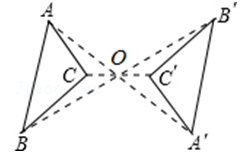 A、点A与点 是对称点 B、 C、AB∥ D、∠ACB=∠17. 如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A、点A与点 是对称点 B、 C、AB∥ D、∠ACB=∠17. 如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE18. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B的度数为( )
A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE18. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B的度数为( )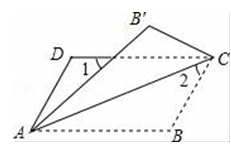 A、102° B、108° C、114° D、124°
A、102° B、108° C、114° D、124°三、解答题(本大题共有4小题,共计46分.解答时应写出必要的文字说明、证明过程或演算步骤.)
-
19. 某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.(1)、当n为何值时,男生小强参加是确定事件?(2)、当n为何值时,男生小强参加是随机事件?20. 中华文明源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000 名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如图所示的不完整的统计图表:

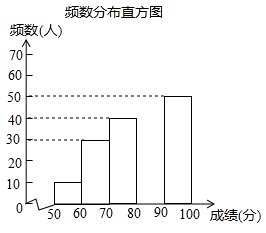
根据所给信息,解答下列问题:
(1)、m= , n=;(2)、补全频数分布直方图;(3)、若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?