江苏省镇江市2020届九年级下学期数学3月月考试卷B卷
试卷更新日期:2020-04-08 类型:月考试卷
一、填空题(本大题共有12小题,每小题3分,共计36分.)
-
1. 已知两个相似三角形的面积比是4:1,则这两个三角形的周长比是.2. 如图,在正方形ABCD中,点E为AD的中点,连接EB,设∠EBA=α,则tanα=.
 3. 已知 ,则=.
3. 已知 ,则=.
4. 如图,△ABC 的 两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =. 5. 如图,平行四边形ABCD的面积为12,E为BC中点,DE、AC交于F点,△DFC的面积为.
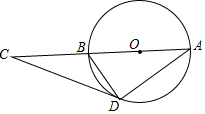
5. 如图,平行四边形ABCD的面积为12,E为BC中点,DE、AC交于F点,△DFC的面积为.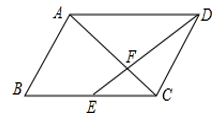 6. 如图,在△ABC中,∠1=∠A,若BD=2,AD=3,则BC=.
6. 如图,在△ABC中,∠1=∠A,若BD=2,AD=3,则BC=. 7. 已知一直立的电线杆在地面上的影长为28m,同时,高为1.4m的测竿在地面上的影长为2.8m,由此可知该电线杆的长为m.8. 如图,正方形ABCD中, E是AD的中点,点F在CD上,且CF=3FD,若 ,则EF的长等于.
7. 已知一直立的电线杆在地面上的影长为28m,同时,高为1.4m的测竿在地面上的影长为2.8m,由此可知该电线杆的长为m.8. 如图,正方形ABCD中, E是AD的中点,点F在CD上,且CF=3FD,若 ,则EF的长等于. 9. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,且 = ,已知点A(﹣1,0),点C( ,1),则A'C'=.
9. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,且 = ,已知点A(﹣1,0),点C( ,1),则A'C'=.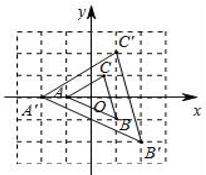 10. 如图,小明同学在东西方向的环海路上的A处,测得海中灯塔P在北偏东60°方向,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=米(结果用根号表示).
10. 如图,小明同学在东西方向的环海路上的A处,测得海中灯塔P在北偏东60°方向,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=米(结果用根号表示). 11. 如图,在△ABC中,sinB= ,tanC= ,AB=3,则AC的长为 .
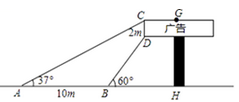
11. 如图,在△ABC中,sinB= ,tanC= ,AB=3,则AC的长为 . 12. 我国自主研发的大型飞机C919成功首飞.如图是某型号飞机机翼的示意图,其中m=1,n= ,则AB的长为 .
12. 我国自主研发的大型飞机C919成功首飞.如图是某型号飞机机翼的示意图,其中m=1,n= ,则AB的长为 .
二、选择题(本大题共有6小题,每小题3分,共计18分.在每小题所给出的四个选项中,恰有一项符合题目要求.)
-
13. 已知sinA= ,那么锐角 等于( )A、15° B、30° C、45° D、60°14. 如图,在△ABC中,点D,E分别在边BA,CA的延长线上, =2,那么下列条件中能判断DE∥BC的是( )
 A、 B、 C、 D、15. 如图,在正方形网格中,△ABC的三个顶点均在格点上,则sin∠CAB的值等于( )
A、 B、 C、 D、15. 如图,在正方形网格中,△ABC的三个顶点均在格点上,则sin∠CAB的值等于( ) A、2 B、 C、 D、16. 如图,在坡度为 的山坡上种树,要求相邻两棵树的水平距离是6m,则斜坡上相邻两棵树的坡面距离是( )
A、2 B、 C、 D、16. 如图,在坡度为 的山坡上种树,要求相邻两棵树的水平距离是6m,则斜坡上相邻两棵树的坡面距离是( ) A、3m B、3 m C、12m D、6m17. 一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )
A、3m B、3 m C、12m D、6m17. 一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( ) A、(30 -50,30) B、(30,30 -50) C、(30 ,30) D、(30,30 )18. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( )
A、(30 -50,30) B、(30,30 -50) C、(30 ,30) D、(30,30 )18. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题(本大题共有4小题,共计46分.解答时应写出必要的文字说明、证明过程或演算步骤.)
-
19.(1)、完成下列表格,并回答下列问题,
锐角
(2)、当锐角 逐渐增大时, 的值逐渐 , 的值逐渐 , 的值逐渐 .(3)、 , ;(4)、 ;(5)、 ;(6)、若 ,则锐角 .