江苏省镇江市2020届九年级下学期数学3月月考试卷A卷
试卷更新日期：2020-04-08 类型：月考试卷
一、填空题（本大题共有12小题，每小题3分，共计36分．）
-
1. 已知 = ，则 的值为.2. 在Rt△ABC中，∠C=90°，sinA= ，那么cosA= ．3. 如图，在△ABC中，DE∥BC，若AD=3，DB=5，DE=3.3，那么BC=.
4.如图，若点A的坐标为(1， )，则sin∠1=
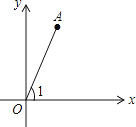5. 如图，在一次数学课外实践活动中，小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°，测角仪高AD为1m，则旗杆高BC为m．（结果保留根号）
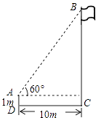6. 如图，△ABC中，A、B两个顶点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．已知点B′的坐标是（3，﹣1），则点B的坐标是.
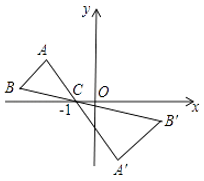7. 如图，菱形ABCD的对角线AC，BD相交于点O．若tan∠BAC= ，AC=6，则BD的长是.
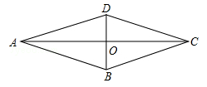8. 如图，在一次测绘活动中，小华同学站在点A的位置观测停泊于B、C两处的小船，测得船B在点A北偏东75°方向900米处，船C在点A南偏东15°方向1200米处，则船B与船C之间的距离为米．
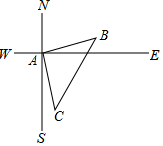9.如图，在5×5的正方形网格中，△ABC的三个顶点A，B，C均在格点上，则tanA的值为
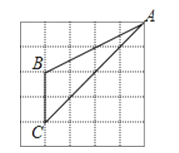10. 如图，AD∥BC，∠D=90°，AD=2，BC=6，DC=8，若在边DC上有点P，使△PAD与△PBC相似，则这样的点P有个．
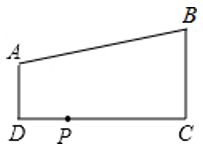11. 在平行四边形ABCD中，E为CD的中点，△DOE的面积是2，△DOA的面积 ．
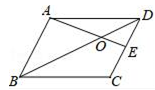12. 如图，在矩形ABCD中，点E是CD的中点，将△BCE沿BE折叠后得到△BEF，点F在矩形ABCD的内部，将BF延长交AD于点G．若 = ，则 = ．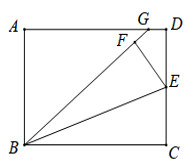
二、选择题（本大题共有6小题，每小题3分，共计18分．在每小题所给出的四个选项中，恰有一项符合题目要求．）
-
13. Rt△ABC中，如果各边长度都扩大 倍，则锐角A的各个三角函数值（ ）A、不变化 B、扩大2倍 C、缩小 D、不能确定14.
如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1：2.5，斜坡CD的坡角为30度，则坝底AD的长度为（ ）
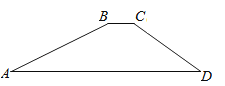A、56米 B、66米 C、（56+20）米 D、（50+20）米15. 如图，为了估计某一条河的宽度，在河的对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S在一条直线上，且直线PS与河垂直，在过点S且与PS垂直的直线a上选择适当的点T，PT与过点Q且与PS垂直的直线b的交点为R，如果QS = 60m，ST =120m，QR=80m，则这条河的宽度PQ为（ ）
A、40m B、120m C、60m D、180m16. 如图，已知AB∥CD∥EF ， AD：AF=3：5，BE=12，那么CE的长等于（ ）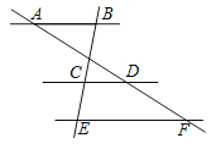
A、 B、 C、 D、17. 如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长交BC边的延长线于E点，对角线BD交AG于F点．已知FG=2，则线段AE的长度为（ ）
A、6 B、8 C、10 D、1218. 如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）都为4m．如果在坡度为0.75的山坡上种树，也要求株距为4m，那么相邻两树间的坡面距离为（ ）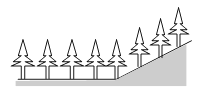
A、5m B、6m C、7m D、8m三、解答题（本大题共有4小题,共计46分．解答时应写出必要的文字说明、证明过程或演算步骤．）
-
19. 在下列三个正方形网格图中，△ABC的顶点和另两条线段的端点都在格点上，以给定的线段为一边，画一个三角形，使所画的三角形都与△ABC相似．（在图2和图3中选择其中一个作答）
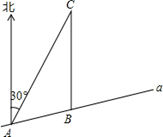
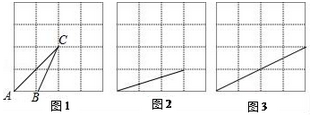20.如图，某船向正东航行，在A处望见海岛C在北偏东60°，前进6海里到B点，此时测得海岛C在北偏东45°，已知在该岛周围6海里内有暗礁，问船继续向正东航行，有触礁的危险吗?
