湖北省武汉市江夏区2020年数学中考模拟试卷(3月)
试卷更新日期:2020-04-08 类型:中考模拟
一、单选题
-
1. 计算-1+4是( )A、 B、 C、3 D、52. 若反比例函数y= 的图象经过点(2,-1),则该反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限3. 点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)都在反比例函数 的图象上,且x1<x2<0<x3 , 则y1、y2、y3的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y34. 若反比例函数 与一次函数 的图像没有交点,则 的值可以是( )
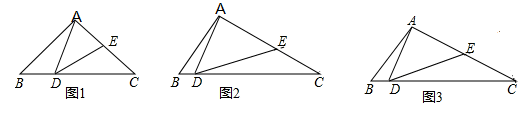
A、-2 B、-1 C、1 D、25. 如图,A、C是函数y= 的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1 , Rt△COD的面积为S2 , 则( )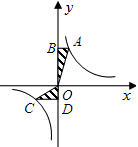 A、S1>S2 B、S1<S2 C、S1=S2 D、S1和S2的大小关系不能确定6. 如图,在正三角形ABC中,点D、E分别在AC、AB上,且 ,AE=BE,则有( )
A、S1>S2 B、S1<S2 C、S1=S2 D、S1和S2的大小关系不能确定6. 如图,在正三角形ABC中,点D、E分别在AC、AB上,且 ,AE=BE,则有( )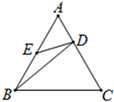 A、△AED∽△BED B、△AED∽△CBD C、△AED∽△ABD D、△BAD∽△BCD7. 下列说法中正确的是( )A、位似图形可以通过平移而相互得到 B、位似图形的对应边平行且相等 C、位似图形的位似中心不只有一个 D、位似中心到对应点的距离之比都相等8. 如图,正比例函数 和反比例函数 的图象交于 ,B两点,给出下列结论:① ;②当 时, ;③当 时, ;④当 时, 随x的增大而减小.其中正确的个数为( )
A、△AED∽△BED B、△AED∽△CBD C、△AED∽△ABD D、△BAD∽△BCD7. 下列说法中正确的是( )A、位似图形可以通过平移而相互得到 B、位似图形的对应边平行且相等 C、位似图形的位似中心不只有一个 D、位似中心到对应点的距离之比都相等8. 如图,正比例函数 和反比例函数 的图象交于 ,B两点,给出下列结论:① ;②当 时, ;③当 时, ;④当 时, 随x的增大而减小.其中正确的个数为( )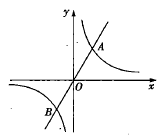 A、0 B、1 C、2 D、39. 将一副三角板按如图叠放, 是等腰直角三角形, 是有一个角为 的直角三角形,则 与 的面积之比等于( )
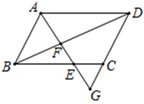
A、0 B、1 C、2 D、39. 将一副三角板按如图叠放, 是等腰直角三角形, 是有一个角为 的直角三角形,则 与 的面积之比等于( ) A、 B、 C、 D、10. 如图, 是 的直径, 切 于点 , ,点 在 上, 交 于 , ,则 的长是( )
A、 B、 C、 D、10. 如图, 是 的直径, 切 于点 , ,点 在 上, 交 于 , ,则 的长是( )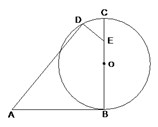 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
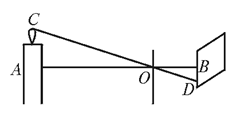
11. 已知一个正比例函数的图象与一个反比例函数图象的一个交点坐标为(1,3),则另一个交点坐标是.12. 如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm, OB=15 cm,则火焰的长度为.
 13. 在Rt△ABC中,∠ C=90°,sinA= ,AC=24,则AB=.14. 若点A(-2,-2)在反比例函数 的图象上,则当函数值y≥-2时,自变量x的取值范围是15. 如图,在平面直角坐标系中,函数y= (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为.
13. 在Rt△ABC中,∠ C=90°,sinA= ,AC=24,则AB=.14. 若点A(-2,-2)在反比例函数 的图象上,则当函数值y≥-2时,自变量x的取值范围是15. 如图,在平面直角坐标系中,函数y= (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为.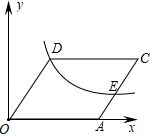 16. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O意旋转.当 时. 的值为.
16. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O意旋转.当 时. 的值为.
三、解答题
-
17. 已知双曲线 的图像经过点A(3,4).(1)、求k的值;(2)、请判断点B(2,6)是否在这个反比例函数的图象上,并说明理由.18. 如图,▱ABCD中,E为BC边的中点,连AE并与DC的延长线交于点F,求证:DC=CF.
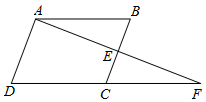 19. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .
19. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .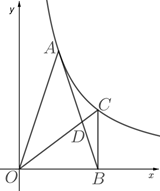 (1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.
(1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.