湖南省邵阳市2019-2020学年高三理数第一次联考试卷
试卷更新日期:2020-04-07 类型:高考模拟
一、单选题
-
1. 在复平面内,复数 z=cos3+isin3( i 是虚数单位)对应的点位于 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 设 ,则“ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 在四边形 ( )A、 B、 C、 D、4. 若x,y满足约束条件 的取值范围是( )A、[0,6] B、[0,4] C、[6, D、[4,5. 一个几何体的三视图如图所示,则该几何体的体积为( )
 A、 B、 C、 D、6. 函数 与 在同一直角坐标系下的图象大致是( )A、
A、 B、 C、 D、6. 函数 与 在同一直角坐标系下的图象大致是( )A、 B、
B、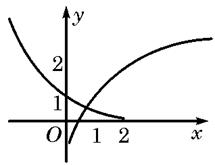 C、
C、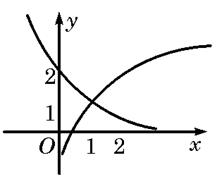 D、
D、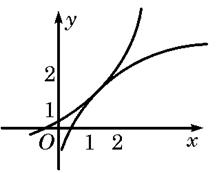 7. 已知奇函数 在 上是增函数,若 ,则 的大小关系为( )A、 B、 C、 D、8. 设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m= ( )A、5 B、6 C、7 D、89. 已知点 是直线 上动点,过点 引圆 两条切线 , 为切点,当 的最大值为 时,则 的值为( )A、 B、 C、 D、10. 英国统计学家 辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
7. 已知奇函数 在 上是增函数,若 ,则 的大小关系为( )A、 B、 C、 D、8. 设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m= ( )A、5 B、6 C、7 D、89. 已知点 是直线 上动点,过点 引圆 两条切线 , 为切点,当 的最大值为 时,则 的值为( )A、 B、 C、 D、10. 英国统计学家 辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):法官甲
终审结果
民事庭
行政庭
合计
维持
29
100
129
推翻
3
18
21
合计
32
118
150
法官乙
终审结果
民事庭
行政庭
合计
维持
90
20
110
推翻
10
5
15
合计
100
25
125
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为 , 和 ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为 , 和 ,则下面说法正确的是( )
A、 , , B、 , , C、 , , D、 , ,11. 已知双曲线 的右顶点为 ,抛物线 的焦点为 .若在 的渐近线上存在点 ,使得 ,则 的离心率的取值范围是 ( )A、 B、 C、 D、12. 在正四棱锥 中,已知异面直线 与 所成的角为 ,给出下面三个命题::若 ,则此四棱锥的侧面积为 ;
:若 分别为 的中点,则 平面 ;
:若 都在球 的表面上,则球 的表面积是四边形 面积的 倍.
在下列命题中,为真命题的是( )
A、 B、 C、 D、二、填空题
-
13. 已知 为三角形内角, ,则 .14. 已知函数 ,若存在四个不同的实数 满足 ,且 ,则 .15. 为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:
(i)老年人的人数多于中年人的人数;
(ii)中年人的人数多于青年人的人数;
(iii)青年人的人数的两倍多于老年人的人数.
①若青年人的人数为4,则中年人的人数的最大值为.
②抽取的总人数的最小值为 .
16. 太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:能够将圆 的周长和面积同时等分成两个部分的函数称为圆 的一个“太极函数”,则下列有关说法中:
①对于圆 的所有非常数函数的太极函数中,都不能为偶函数;
②函数 是圆 的一个太极函数;
③直线 所对应的函数一定是圆 的太极函数;
④若函数 是圆 的太极函数,则
所有正确的是 .
三、解答题
-
17. 在 中,角 所对的边为 ,且 .(1)、求角 的大小;(2)、若 ,求 的取值范围.18. 已知正项数列 中, .(1)、求数列 的通项公式;(2)、若数列 是等差数列,且 , ,求数列 的前 项和 .19. 已知菱形 的边长为 , , ,将菱形 沿对角线 折起,使 ,得到三棱锥 ,如图所示.

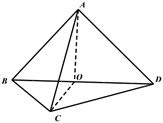 (1)、当 时,求证: 平面 ;(2)、当二面角 的大小为 时,求直线 与平面 所成的正切值.20. 半圆 的直径的两端点为 ,点 在半圆 及直径 上运动,若将点 的纵坐标伸长到原来的2倍(横坐标不变)得到点 ,记点 的轨迹为曲线 .(1)、求曲线 的方程;(2)、若称封闭曲线上任意两点距离的最大值为该曲线的“直径”,求曲线 的“直径”.21. 某地政府为了帮助当地农民脱贫致富,开发了一种新型水果类食品,该食品生产成本为每件8元.当天生产当天销售时,销售价为每件12元,当天未卖出的则只能卖给水果罐头厂,每件只能卖5元.每天的销售量与当天的气温有关,根据市场调查,若气温不低于 ,则销售5000件;若气温位于 ,则销售3500件;若气温低于 ,则销售2000件.为制定今年8月份的生产计划,统计了前三年8月份的气温范围数据,得到下面的频数分布表:
(1)、当 时,求证: 平面 ;(2)、当二面角 的大小为 时,求直线 与平面 所成的正切值.20. 半圆 的直径的两端点为 ,点 在半圆 及直径 上运动,若将点 的纵坐标伸长到原来的2倍(横坐标不变)得到点 ,记点 的轨迹为曲线 .(1)、求曲线 的方程;(2)、若称封闭曲线上任意两点距离的最大值为该曲线的“直径”,求曲线 的“直径”.21. 某地政府为了帮助当地农民脱贫致富,开发了一种新型水果类食品,该食品生产成本为每件8元.当天生产当天销售时,销售价为每件12元,当天未卖出的则只能卖给水果罐头厂,每件只能卖5元.每天的销售量与当天的气温有关,根据市场调查,若气温不低于 ,则销售5000件;若气温位于 ,则销售3500件;若气温低于 ,则销售2000件.为制定今年8月份的生产计划,统计了前三年8月份的气温范围数据,得到下面的频数分布表:气温范围
(单位: )
天数
4
14
36
21
15
以气温范围位于各区间的频率代替气温范围位于该区间的概率.
(1)、求今年8月份这种食品一天销售量(单位:件)的分布列和数学期望值;(2)、设8月份一天销售这种食品的利润为 (单位:元),当8月份这种食品一天生产量 (单位:件)为多少时, 的数学期望值最大,最大值为多少22. 已知函数 为反比例函数,曲线 在 处的切线方程为 .(1)、求 的解析式;(2)、判断函数 在区间 内的零点的个数,并证明.