湖南省汨罗市2020届高三理数教学质量检测试卷(一)
试卷更新日期:2020-04-07 类型:高考模拟
一、单选题
-
1. 已知全集 ,集合 ,集合 ,则 ( )A、 B、 C、 D、2. 已知实数 , ,则“ ”是“ ”的( )A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件3. 在等比数列 中,若 , , 成等差数列,则公比q为( )A、1 B、2 C、1或 D、4. 如图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为 .如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
 A、9 B、10 C、11 D、125. 若直线 截得圆 的弦长为 ,则 的最小值为( )A、 B、 C、 D、6. 我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.如函数 的图象大致是( )A、
A、9 B、10 C、11 D、125. 若直线 截得圆 的弦长为 ,则 的最小值为( )A、 B、 C、 D、6. 我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.如函数 的图象大致是( )A、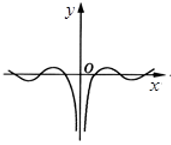 B、
B、 C、
C、 D、
D、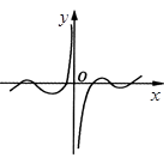 7. 函数 的图像可由函数 的图像至少向右平移( )个单位长度得到.A、 B、 C、 D、8. 若向量 与 的夹角为 , , ,则 =( )A、
7. 函数 的图像可由函数 的图像至少向右平移( )个单位长度得到.A、 B、 C、 D、8. 若向量 与 的夹角为 , , ,则 =( )A、 B、1
C、4
D、3
9. 如图, 和 是圆 两条互相垂直的直径,分别以 , , , 为直径作四个圆,在圆 内随机取一点,则此点取自阴影部分的概率是( )
B、1
C、4
D、3
9. 如图, 和 是圆 两条互相垂直的直径,分别以 , , , 为直径作四个圆,在圆 内随机取一点,则此点取自阴影部分的概率是( )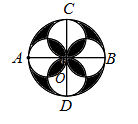 A、 B、 C、 D、10. 设函数 的定义域为 ,满足 ,且当 时, .若对任意 ,都有 ,则 的取值范围是( )A、 B、 C、 D、11. 是球 的直径, 、 是该球面上两点, , ,棱锥 的体积为 ,则球 的表面积为( )A、 B、 C、 D、12. 关于函数 ,下列说法正确的是( )
A、 B、 C、 D、10. 设函数 的定义域为 ,满足 ,且当 时, .若对任意 ,都有 ,则 的取值范围是( )A、 B、 C、 D、11. 是球 的直径, 、 是该球面上两点, , ,棱锥 的体积为 ,则球 的表面积为( )A、 B、 C、 D、12. 关于函数 ,下列说法正确的是( )
(1) 是 的极小值点;(2)函数 有且只有1个零点;(3) 恒成立;(4)设函数 ,若存在区间 ,使 在 上的值域是 ,则 .A、(1) (2) B、(2)(4) C、(1) (2) (4) D、(1)(2)(3)(4)二、填空题
-
13. 已知单位向量 与向量 方向相同,则向量 的坐标是.14. 已知 中,a , b , c分别是角A , B , C的对边,若 , ,则 的值为.15. 2019年1月1日起新的个人所得税法开始实施,依据《中华人民共和国个人所得税法》可知纳税人实际取得工资、薪金(扣除专项、专项附加及依法确定的其他)所得不超过5000元(俗称“起征点”)的部分不征税,超出5000元部分为全月纳税所得额.新的税率表如下:
2019年1月1日后个人所得税税率表
全月应纳税所得额
税率(%)
不超过3000元的部分
3
超过3000元至12000元的部分
10
超过12000元至25000元的部分
20
超过25000元至35000元的部分
25
个人所得税专项附加扣除是指个人所得税法规定的子女教育、继续教育、大病医疗、住房贷款利息、住房租金和赡养老人等六项专项附加扣除.其中赡养老人一项指纳税人赡养60岁(含)以上父母及其他法定赡养人的赡养支出,可按照以下标准扣除:纳税人为独生子女的,按照每月2000元的标准定额扣除;纳税人为非独生子女的,由其与兄弟姐妹分摊每月2000元的扣除额度,每人分摊的额度不能超过每月1000元.某纳税人为独生子,且仅符合规定中的赡养老人的条件,如果他在2019年10月份应缴纳个人所得税款为390元,那么他当月的工资、薪金税后所得是元.
16. 函数 的最大值是.三、解答题
-
17. 已知等差数列 的前n项和为 ,公差d为整数, ,且 , , 成等比数列.(1)、求数列 的通项公式;(2)、设数列 满足 ,求数列 的前n项和 .18. 已知四棱锥 , , , , , , 平面 .
 (1)、求证:平面 平面 ;(2)、当 时,求直线 和平面 所成角的正弦值.19. 已知椭圆 ( )的离心率为 ,短轴长为 .
(1)、求证:平面 平面 ;(2)、当 时,求直线 和平面 所成角的正弦值.19. 已知椭圆 ( )的离心率为 ,短轴长为 .(Ⅰ)求椭圆 的标准方程;
(Ⅱ)若直线 与椭圆 交于不同的两点 ,且线段 的垂直平分线过定点 ,求实数 的取值范围.
20. 已知函数 .(1)、若函数 的图象与x轴相切,求实数a的值;(2)、讨论函数 的零点个数.21. 冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征( )和严重急性呼吸综合征( )等较严重疾病.而今年出现在湖北武汉的新型冠状病毒( )是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n( )份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验n次.
方式二:混合检验,将其中k( 且 )份血液样本分别取样混合在一起检验.
若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为 .
假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p( ).现取其中k( 且 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为 ,采用混合检验方式,样本需要检验的总次数为 .
(1)、若 ,试求p关于k的函数关系式 ;(2)、若p与干扰素计量 相关,其中 ( )是不同的正实数,满足 且 ( )都有 成立.
(i)求证:数列 等比数列;
(ii)当 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值