山东省临沂市河东区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-04 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各图能表示y是x的函数是（　　）

A、 B、 C、 D、

查看试题解析
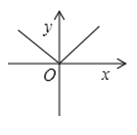2. 下列各式中正确的是（）

A、 $\sqrt{16}$ =±4 B、 $\sqrt{{(- 2)}^{2}}$ =2 C、 $\sqrt{27}$ =3 D、 $\frac{1}{\sqrt{3}}$ = $\sqrt{3}$

查看试题解析
3. 在端午节到来之前，学校食堂推荐了A，B，C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购，下面的统计量中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
4. 下列各组数据中的三个数，可作为三边长构成直角三角形的是（）

A、4，5，6 B、2，3，4 C、11，12，13 D、8，15，17

查看试题解析
5. 将一次函数y=﹣2x+4的图象平移得到图象的函数关系式为y=﹣2x，则移动方法为（）

A、向左平移4个单位 B、向右平移4个单位 C、向上平移4个单位 D、向下平移4个单位

查看试题解析
6. 如图，在▱ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（）

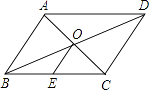A、3cm B、6cm C、9cm D、12cm

查看试题解析
7. 如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（）

A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+3

查看试题解析
8. 如图，在数轴上点A表示的数为a，则a的值为（）

A、 $\sqrt{5}$ B、﹣ $\sqrt{5}$ C、1﹣ $\sqrt{5}$ D、﹣1+ $\sqrt{5}$

查看试题解析
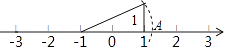9. 如图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中x表示时间，y表示张强离家的距离．根据图象提供的信息，以下四个说法错误的是（）

A、体育场离张强家3.5千米 B、张强在体育场锻炼了15分钟 C、体育场离早餐店1.5千米 D、张强从早餐店回家的平均速度是3千米/小时

查看试题解析
10. 如图，在菱形ABCD中，E是AB边上一点，且∠A=∠EDF=60°，有下列结论：①AE=BF；②△DEF是等边三角形；③△BEF是等腰三角形；④∠ADE=∠BEF，其中结论正确的个数是（）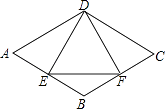

A、3 B、4 C、1 D、2

查看试题解析
11.
将2×2的正方形网格如图放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，正方形ABCD的顶点都在格点上．若直线y=kx（k≠0）与正方形ABCD有公共点，则k的取值范围是（）

A、k≤2 B、 $k \geq \frac{1}{2}$ C、 $\frac{1}{2} \leq k \leq 2$ D、 $\frac{1}{2} < k < 2$

查看试题解析

二、填空题：

12. 如果 $\sqrt{1 - x}$ 有意义，那么字母x的取值范围是．

查看试题解析
13. 点（﹣1，y₁）、（2，y₂）是直线y=2x+1上的两点，则y₁y₂（填“＞”或“=”或“＜”）．

查看试题解析
14. 如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为 cm² ．

查看试题解析
15. 已知两条线段的长分别为 $\sqrt{2}$ cm、 $\sqrt{3}$ cm，那么能与它们组成直角三角形的第三条线段的长是．

查看试题解析
16. 如图，△ABC中，AB=AC，BC=12cm，点D在AC上，DC=4cm．将线段DC沿着CB的方向平移7cm得到线段EF，点E，F分别落在边AB，BC上，则△EBF的周长为 cm．

查看试题解析
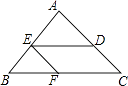17.
一次函数y₁=kx+b与y₂=x+a的图象如图，则下列结论：①k＜0；②a＞0；③关于x的方程kx﹣x=a﹣b的解是x=3；④当x＜3时，y₁＜y₂中．则正确的序号有．

查看试题解析
18. 如图，矩形纸片ABCD中，AD=1，将纸片折叠，使顶点A与CD边上的点E重合，折痕FG分别与AD、AB交于点F、G，若DE= $\frac{\sqrt{3}}{3}$ ，则EF的长为．

查看试题解析
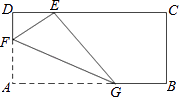19. 在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为．

查看试题解析

三、解答题：

20. 计算：（2 $\sqrt{3}$ ﹣ $\sqrt{6}$ ）²+（ $\sqrt{54}$ +2 $\sqrt{6}$ ）÷ $\sqrt{3}$ ．

查看试题解析
21. 某校为了备战2018体育中考，因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试，测试的情况绘制成表格如下：
个数
16
22
25
28
29
30
35
37
40
42
45
46
人数
2
1
7
18
1
9
5
2
1
1
1
2

(1)、通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是，请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数，它们分别是、．

(2)、学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次，已知该校五年级有女生250名，试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少？

查看试题解析
22.
在平面直角坐标系中，现将一块等腰直角三角板ABC放在第一象限，斜靠在两条坐标轴上，且点A（0，2），点C（1，0），BE⊥x轴于点E，一次函数y=x+b经过点B，交y轴于点D．

(1)、求证：△AOC≌△CEB；

(2)、求△ABD的面积．

查看试题解析
23. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

(1)、求证：△ABM≌△DCM；

(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)、当AD：AB=时，四边形MENF是正方形（只写结论，不需证明）．

查看试题解析
24. 某校实行学案式教学，需印制若干份数学学案，印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示：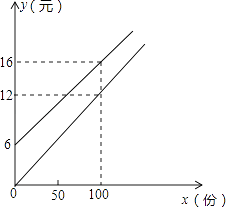

(1)、填空：甲种收费的函数关系式是．
乙种收费的函数关系式是．

(2)、该校某年级每次需印制100～450（含100和450）份学案，选择哪种印刷方式较合算？

查看试题解析
25.
如图①，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在AD、AF上，此时BD=CF，BD⊥CF成立．

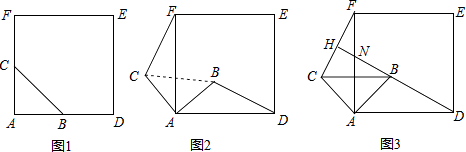(1)、如图②，
i）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，线段BD与线段CF的数量关系是；直线BD与直线CF的位置关系是．
ii）请利用图②证明上述结论．

(2)、如图③，当△ABC绕点A逆时针旋转45°时，延长DB交CF于点H，若AB= $\sqrt{2}$ ，AD=3时，求线段FC的长．

查看试题解析

个数	16	22	25	28	29	30	35	37	40	42	45	46
人数	2	1	7	18	1	9	5	2	1	1	1	2