山东省济宁市汶上县2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-04 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 在函数 自变量x的取值范围是( )A、 B、 C、 D、2. 某商场试销一种新款衬衫,一周内售出型号记录情况如表所示:
型号(厘米)
38
39
40
41
42
43
数量(件)
25
30
36
50
28
8
商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是( )
A、平均数 B、中位数 C、众数 D、方差3. 下列运算中错误的是( )A、 + = B、 × = C、 ÷ =2 D、 =34. 一次函数y=ax+b(a<0)图象上有A、B两点,A(x1 , y1),B(x2 , y2),且x1>x2 , 则y1和y2的大小关系为( )A、y1>y2 B、y1<y2 C、y1=y2 D、无法判断5. 已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )A、选①② B、选①③ C、选②④ D、选②③6. 如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( ) A、36 B、40 C、 D、387. 如图,已知矩形ABCD中,R,P分别是DC、BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
A、36 B、40 C、 D、387. 如图,已知矩形ABCD中,R,P分别是DC、BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,那么下列结论成立的是( )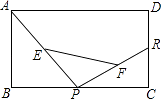 A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不改变 D、线段EF的长不能确定8.
A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不改变 D、线段EF的长不能确定8.如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
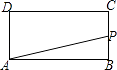
D、 9. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( )
9. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( ) A、4 B、6 C、8 D、1010. 如图,直线y=kx+b经过A(3,1)和B(6,0)两点,则不等式组0<kx+b< x的解集为( )
A、4 B、6 C、8 D、1010. 如图,直线y=kx+b经过A(3,1)和B(6,0)两点,则不等式组0<kx+b< x的解集为( ) A、3<x<6 B、x>3 C、x<6 D、x>3或x<6
A、3<x<6 B、x>3 C、x<6 D、x>3或x<6二、填空题
-
11. 若 =3﹣x,则x的取值范围是 .12. 已知函数:y= ,当x=2时,函数值y为 .
13. 某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学习的平均时间是小时. 14. 如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是 .
14. 如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是 . 15.
15.在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 .

三、解答题
-
16. 计算: .17.
某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
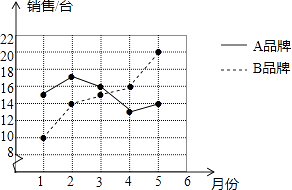 (1)、分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;(2)、根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.18. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)、分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;(2)、根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.18. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.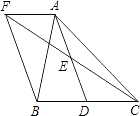 (1)、求证:BD=CD;(2)、如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.19. 【知识链接】
(1)、求证:BD=CD;(2)、如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.19. 【知识链接】有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如: 的有理化因式是 ;1﹣ 的有理化因式是1+ .
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:
= = ﹣1, = = ﹣ .
(1)、【知识理解】填空:2 的有理化因式是;
直接写出下列各式分母有理化的结果:
① =;② = .
(2)、【启发运用】计算: + + +…+ .
20. 如图,在平面直角坐标系xOy中,已知正比例函数y= x与一次函数y=﹣x+7的图象交于点A. (1)、求点A的坐标;(2)、设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= x和y=﹣x+7的图象于点B、C,连接OC.若BC= OA,求△OBC的面积.21. 我市某西瓜产地组织40辆汽车装运完A,B,C三种西瓜共200吨到外地销售.按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满.根据下表提供的信息,解答以下问题:
(1)、求点A的坐标;(2)、设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= x和y=﹣x+7的图象于点B、C,连接OC.若BC= OA,求△OBC的面积.21. 我市某西瓜产地组织40辆汽车装运完A,B,C三种西瓜共200吨到外地销售.按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满.根据下表提供的信息,解答以下问题:西瓜种类
A
B
C
每辆汽车运载量(吨)
4
5
6
每吨西瓜获利(百元)
16
10
12
(1)、设装运A种西瓜的车辆数为x辆,装运B种西瓜的车辆数为y辆,求y与x的函数关系式;(2)、如果装运每种西瓜的车辆数都不少于10辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)、若要是此次销售获利达到预期利润25万元,应采取怎样的车辆安排方案?22. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H. (1)、求证:EB=GD;(2)、判断EB与GD的位置关系,并说明理由;(3)、若AB=2,AG= ,求EB的长.
(1)、求证:EB=GD;(2)、判断EB与GD的位置关系,并说明理由;(3)、若AB=2,AG= ,求EB的长.