山东省济宁市嘉祥县2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-04 类型:期末考试
一、选择题
-
1. 一组数据2,0,﹣2,1,3的平均数是( )A、0.8 B、1 C、1.5 D、22. 下列各式是最简二次根式的是( )A、 B、 C、 D、3. 下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )A、 B、6、8、10 C、5、12、13 D、4. 下列函数中,y是x的一次函数的是( )
①y=x﹣6;②y=;③y=;④y=7﹣x.
A、①②③ B、①③④ C、①②③④ D、②③④5. 有一直角三角形的两边长分别为3和4,则第三边长是( )A、5 B、5或 C、 D、6. 如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( )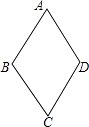 A、52cm B、40cm C、39cm D、26cm7. 如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧秤的读数F(kg)与时间t(s)的函数图象大致是( )
A、52cm B、40cm C、39cm D、26cm7. 如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧秤的读数F(kg)与时间t(s)的函数图象大致是( ) A、
A、 B、
B、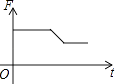 C、
C、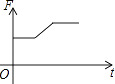 D、
D、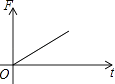 8. 已知一次函数y=kx+b,若k+b=0,则该函数的图象可能( )A、
8. 已知一次函数y=kx+b,若k+b=0,则该函数的图象可能( )A、 B、
B、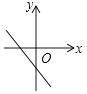 C、
C、 D、
D、 9. 对于函数y=﹣2x+1,下列结论正确的是( )A、它的图象必经过点(﹣1,2) B、它的图象经过第一、二、三象限 C、当x>1时,y<0 D、y的值随x值的增大而增大10. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
9. 对于函数y=﹣2x+1,下列结论正确的是( )A、它的图象必经过点(﹣1,2) B、它的图象经过第一、二、三象限 C、当x>1时,y<0 D、y的值随x值的增大而增大10. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 若代数式 有意义,则x的取值范围是12. 若y=(m﹣1)x|m|是正比例函数,则m的值为13. 若一次函数y=(3﹣k)x﹣k的图象经过第二、三、四象限,则k的取值范围是 .
14. 如图是一段楼梯,高BC是3米,斜边AC是5米,若在楼梯上铺地毯,则至少需要地毯米. 15. 如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是 cm.
15. 如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是 cm.
三、解答题
-
16. 计算:(1)、(2017 +2017 )( ﹣ )(2)、( ﹣4 )﹣(3 ﹣2 )17. 在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
 18. 中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
18. 中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示: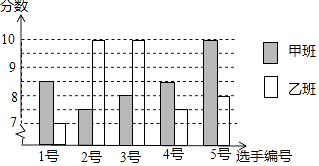 (1)、根据上图填写下表:
(1)、根据上图填写下表:平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8.5
10
1.6
(2)、根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
19. 如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O. (1)、求证:四边形ADCE是矩形.(2)、若∠AOE=60°,AE=4,求矩形ADCE对角线的长.20. 已知直线y=kx+b经过点A(5,0),B(1,4).
(1)、求证:四边形ADCE是矩形.(2)、若∠AOE=60°,AE=4,求矩形ADCE对角线的长.20. 已知直线y=kx+b经过点A(5,0),B(1,4). (1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集.21. 阅读下列解题过程,并解答后面的问题:
(1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集.21. 阅读下列解题过程,并解答后面的问题:如图1,在平面直角坐标系xOy中,A(x1 , y1),B(x2 , y2),C为线段AB的中点,求C点的坐标.
解:分布过A、C做x轴的平行线,过B、C做y轴的平行线,两组平行线的交点如图1所示.
设C(x0 , y0),则D(x0 , y1),E(x2 , y1),F(x2 , y0)
由图1可知:x0= =
y0= =
∴( , )

问题:
(1)、已知A(﹣1,4),B(3,﹣2),则线段AB的中点坐标为(2)、平行四边形ABCD中,点A、B、C的坐标分别为(1,﹣4),(0,2),(5,6),求点D的坐标.(3)、如图2,B(6,4)在函数y= x+1的图象上,A(5,2),C在x轴上,D在函数y= x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标. 22. A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.(1)、设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.(2)、若总运费不超过9000元,问有几种调运方案?(3)、求出总运费最低的调运方案,并求出最低运费.
22. A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.(1)、设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.(2)、若总运费不超过9000元,问有几种调运方案?(3)、求出总运费最低的调运方案,并求出最低运费.