山东省德州市庆云县2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-04 类型:期末考试
一、选择题
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列各组数据中能作为直角三角形的三边长的是( )A、 , , B、1,1, C、4,5,6 D、1, ,23. 矩形、菱形、正方形都具有的性质是( ).A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角4. 下列各曲线表示的y与x的关系中,y不是x的函数的是( )A、
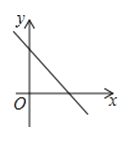 B、
B、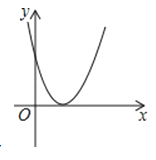 C、
C、 D、
D、 5.
5.已知,一次函数y=kx+b的图象如图,下列结论正确的是( )
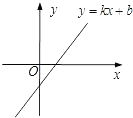 A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<06. 下列计算正确的是( )A、+ = B、﹣3 =1 C、÷ =3 D、3 ×2 =67. 一组数据4,5,7,7,8,6的中位数和众数分别是( )A、7,7 B、7,6.5 C、6.5,7 D、5.5,78. 下列命题中是真命题的有( )个.
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<06. 下列计算正确的是( )A、+ = B、﹣3 =1 C、÷ =3 D、3 ×2 =67. 一组数据4,5,7,7,8,6的中位数和众数分别是( )A、7,7 B、7,6.5 C、6.5,7 D、5.5,78. 下列命题中是真命题的有( )个.①顺次连接任意四边形各边中点得到的四边形是平行四边形;
②三内角之比为3:4:5的三角形是直角三角形;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④对角线互相垂直平分的四边形是正方形;
⑤三边a、b、c满足关系式a2﹣b2=c2的三角形是直角三角形.
A、0 B、1 C、2 D、39. 如果P(2,m),A(1,1),B(4,0)三点在同一直线上,则m的值为( )A、2 B、﹣ C、 D、110. 如图,平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB=1,则EF的长是( ) A、1.5 B、 C、 D、211.
A、1.5 B、 C、 D、211.如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
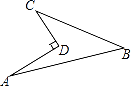 A、96 B、204 C、196 D、30412.
A、96 B、204 C、196 D、30412.如图,在矩形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速运动到点D为止,在这个过程中,下列图象可以大致表示△APD的面积S随点P的运动时间t的变化关系的是( )
 A、
A、 B、
B、 C、
C、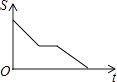 D、
D、
二、填空题
-
13. 将直线y=2x向下平移2个单位,所得函数的图象过第象限.14. 计算: ﹣( ﹣ )= .15. 平行四边形ABCD中,∠ABC的平分线将AD边分成的两部分的长分别为2和3,则平行四边形ABCD的周长是 .16. 如图,在每个小正方形的边长为I的网格中,点A,B,C,D均在格点上,点E在线段BC上,F是线段DB的中点,且BE=DF,则AF的长等于 , AE的长等于 .
 17. 如图设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,此时正方形AEGH的边长为 , 如此下去,则第n个正方形的边长为 .
17. 如图设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,此时正方形AEGH的边长为 , 如此下去,则第n个正方形的边长为 .
三、解答题
-
18. 已知x=2﹣ ,求代数式(7+4 )x2+(2+ )x+ 的值.19.
在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)、此次竞赛中二班成绩在70分及其以上的人数有 人
(2)、补全下表中空缺的三个统计量:平均数(分)
中位数(分)
众数(分)
一班
77.6
80
二班
90
(3)、请根据上述图表对这次竞赛成绩进行分析,写出两个结论.20. 如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形. 21. 如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile
21. 如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile (1)、求PQ,PR的长度;(2)、如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?22. 如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.
(1)、求PQ,PR的长度;(2)、如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?22. 如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E. (1)、判断△EBD的形状,并说明理由;(2)、求DE的长.23. “五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
(1)、判断△EBD的形状,并说明理由;(2)、求DE的长.23. “五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元. (1)、求在甲商店购物时y与x之间的函数关系;(2)、两种购物方式对应的函数图象如图所示,求交点C的坐标;(3)、根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.24. 探究:
(1)、求在甲商店购物时y与x之间的函数关系;(2)、两种购物方式对应的函数图象如图所示,求交点C的坐标;(3)、根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.24. 探究:
(1)、如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标(用含a的代数式表示);
 (2)、
(2)、如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
 (3)、
(3)、如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.
