山东省德州市2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-04 类型：期末考试

进入出卷网下载

一、选择题

1. 若 $\sqrt{3 m - 1}$ 有意义，则m能取的最小整数值是（）

A、m=0 B、m=1 C、m=2 D、m=3

查看试题解析
2. 下列各组数中，以它们为边长的线段不能构成直角三角形的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、3，4，5 C、5，12，13 D、2，2，3

查看试题解析
3. 下列二次根式中属于最简二次根式的是（　　）

A、 $\sqrt{14}$ B、 $\sqrt{48}$ C、 $\sqrt{\frac{a}{b}}$ D、 $\sqrt{4 a + 4}$

查看试题解析
4. 函数y=2x﹣5的图象经过（）

A、第一、三、四象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、二、三象限

查看试题解析
5. 如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB=60°，BD=8，则AB的长为（）

A、4 B、 $4 \sqrt{3}$ C、3 D、5

查看试题解析
6. 如图，正方形ABCD中，AE垂直于BE，且AE=3，BE=4，则阴影部分的面积是（）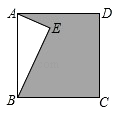

A、16 B、18 C、19 D、21

查看试题解析
7.
某市一周的日最高气温如图所示，则该市这周的日最高气温的众数是（）

A、25 B、26 C、27 D、28

查看试题解析
8. 已知P₁（﹣3，y₁），P₂（2，y₂）是一次函数y=﹣x﹣1的图象上的两个点，则y₁ ， y₂的大小关系是（）

A、y₁=y₂ B、y₁＜y₂ C、y₁_＞y₂ D、不能确定

查看试题解析
9. 2022年将在北京﹣张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数 $\bar{x}$ 与方差s²：
队员1
队员2
队员3
队员4
平均数 $\bar{x}$ （秒）
51
50
51
50
方差s²（秒²）
3.5
3.5
14.5
15.5
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）

A、队员1 B、队员2 C、队员3 D、队员4

查看试题解析
10. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF=12，AB=10，则AE的长为（）

A、13 B、14 C、15 D、16

查看试题解析
11. 如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（）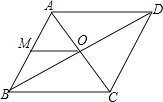

A、5cm B、10cm C、20cm D、40cm

查看试题解析
12. 一次函数y₁=kx+b与y₂=x+a的图象如图，则下列结论①k＜0；②a＞0；③当x＜3时，y₁＜y₂中，正确的个数是（）

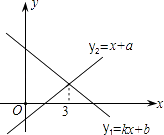A、0 B、1 C、2 D、3

查看试题解析

二、填空题

13. 已知一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是2，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数是．

查看试题解析
14. 函数 $y = \sqrt{x - 3}$ 中，自变量x的取值范围是．

查看试题解析
15. 计算 $a \sqrt{\frac{3}{a}} + \sqrt{9 a} - \frac{3 \sqrt{a}}{\sqrt{3}}$ = ．

查看试题解析
16. 矩形纸片ABCD的边长AB=8，AD=4，将矩形纸片沿EF折叠，使点A与点C重合，折叠后在某一面着色（如图），则着色部分的面积为．

查看试题解析
17. 如图，直线y=kx+b（k≠0）与x轴交于点（﹣4，0），则关于x的方程kx+b=0的解为x= ．

查看试题解析

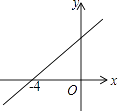
三、解答题

18. 当x= $\frac{1}{\sqrt{2} - 1}$ 时，求x²﹣x+1的值．

查看试题解析
19.
一艘轮船以16海里/时的速度离开港口（如图），向北偏东40°方向航行，另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶，已知它们离港口一个半小时后相距30海里（即BA=30），问另一艘轮船的航行的方向是北偏西多少度？

查看试题解析
20. 已知：如图，点E，F分别为▱ABCD的边BC，AD上的点，且∠1=∠2．
求证：AE=CF．

查看试题解析
21. 阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学生读书册数的情况如表：
读书册数
4
5
6
7
8
人数（人）
6
4
10
12
8
根据表中的数据，求：

(1)、该班学生读书册数的平均数；

(2)、该班学生读书册数的中位数．

查看试题解析
22. 世界上大部分国家都使用摄氏温度（℃），但美国、英国等国家的天气预报使用华氏温度（℉）．两种计量之间有如表对应：
摄氏温度x（℃）
…
0
5
10
15
20
25
…
华氏温度y（℉）
…
32
41
50
59
68
77
…
已知华氏温度y（℉）是摄氏温度x（℃）的一次函数．

(1)、求该一次函数的表达式；

(2)、当华氏温度﹣4℉时，求其所对应的摄氏温度．

查看试题解析
23. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．

(1)、求证：四边形OCED是菱形；

(2)、若∠BAC=30°，AC=4，求菱形OCED的面积．

查看试题解析
24. 已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．

(1)、求甲车离出发地的距离y_甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

(2)、它们出发 $\frac{9}{2}$ 小时时，离各自出发地的距离相等，求乙车离出发地的距离y_乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

(3)、在（2）的条件下，求它们在行驶的过程中相遇的时间．

查看试题解析

	队员1	队员2	队员3	队员4
平均数 $\bar{x}$ （秒）	51	50	51	50
方差s²（秒²）	3.5	3.5	14.5	15.5

摄氏温度x（℃）	…	0	5	10	15	20	25	…
华氏温度y（℉）	…	32	41	50	59	68	77	…

读书册数	4	5	6	7	8
人数（人）	6	4	10	12	8