海南省2020届高三数学第一次联考试卷
试卷更新日期:2020-04-07 类型:高考模拟
一、单选题
-
1. 已知集合 A,则集合 ( )A、 B、 C、 D、2. 命题“ ”的否定为( )A、 B、 C、 D、3. 设集合 、 是全集 的两个子集,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知函数 的导函数 ,当 时, 取极大值1,则函数 的极小值为( )A、 B、1 C、 D、25. 已知函数 ,若 ,则 的取值范围是( )A、 B、 C、 D、6. 已知 ; ,则下列说法中正确的是( )A、 真 真 B、 假 假 C、 真 假 D、 假 真7. 已知集合 ,定义集合 ,则 等于( )A、 B、 C、 D、8. 函数 的图象大致是( )A、
 B、
B、 C、
C、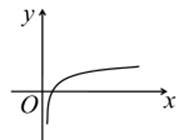 D、
D、 9. 已知定义在 上的奇函数 和偶函数 满足 ( 且 ),若 ,则函数 的单调递增区间为( )A、 B、 C、 D、10. 如图是二次函数 的部分图象,则函数 的零点所在的区间是( )
9. 已知定义在 上的奇函数 和偶函数 满足 ( 且 ),若 ,则函数 的单调递增区间为( )A、 B、 C、 D、10. 如图是二次函数 的部分图象,则函数 的零点所在的区间是( ) A、 B、 C、 D、11. 对于任意 ,函数 满足 ,且当 时,函数 .若 ,则 大小关系是( )A、 B、 C、 D、12. 已知函数 ,则 在 上不单调的一个充分不必要条件可以是( )A、 B、 C、 或 D、
A、 B、 C、 D、11. 对于任意 ,函数 满足 ,且当 时,函数 .若 ,则 大小关系是( )A、 B、 C、 D、12. 已知函数 ,则 在 上不单调的一个充分不必要条件可以是( )A、 B、 C、 或 D、二、填空题
-
13. 如图,直线 是曲线 在 处的切线,则 .
 14. 已知集合 ,若 ,且 ,则实数 所有的可能取值构成的集合是.15. 设函数 在区间 上的值域是 ,则 的取值范围是.16. 已知函数 ,若函数 只有一个零点 ,且 ,则实数 的取值范围.
14. 已知集合 ,若 ,且 ,则实数 所有的可能取值构成的集合是.15. 设函数 在区间 上的值域是 ,则 的取值范围是.16. 已知函数 ,若函数 只有一个零点 ,且 ,则实数 的取值范围.三、解答题
-
17. 已知集合 ,集合 .(1)、求集合 ;(2)、若 ,求实数 的取值范围.18. 已知 , ; , .(1)、若 为真命题,求实数 的取值范围;(2)、若 与 的真假性相同,求实数 的取值范围.19. 已知函数 ,若函数 .(1)、求函数 的定义域;(2)、求函数 的最值.