河南省安阳市林州市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-04 类型:期末考试
一、选择题
-
1. 二次根式 有意义的条件是( )A、x>2 B、x<2 C、x≥2 D、x≤22. 下列计算正确的是( )A、 =±2 B、 C、2 ﹣ =2 D、3. 已知k>0,b<0,则直线y=kx﹣b的大致图象是( )
A、 B、
B、 C、
C、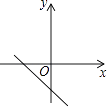 D、
D、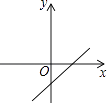 4. 在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在下列关系中,不属于直角三角形的是( )A、b2=a2﹣c2 B、a:b:c=3:4:5 C、∠A﹣∠B=∠C D、∠A:∠B:∠C=3:4:55. 菱形的两条对角线长分别为9cm与4cm,则此菱形的面积为( )cm2 .A、12 B、18 C、20 D、366. 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
4. 在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在下列关系中,不属于直角三角形的是( )A、b2=a2﹣c2 B、a:b:c=3:4:5 C、∠A﹣∠B=∠C D、∠A:∠B:∠C=3:4:55. 菱形的两条对角线长分别为9cm与4cm,则此菱形的面积为( )cm2 .A、12 B、18 C、20 D、366. 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( ) A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC7.
A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC7.如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )
 A、80° B、75° C、70° D、60°8. 如图,折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法,其中正确的说法是( )
A、80° B、75° C、70° D、60°8. 如图,折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法,其中正确的说法是( ) A、汽车共行驶了120千米 B、汽车自出发后前3小时的平均行驶速度为40千米/时 C、汽车在整个行驶过程中的平均速度为40千米/时 D、汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少9. 如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( )
A、汽车共行驶了120千米 B、汽车自出发后前3小时的平均行驶速度为40千米/时 C、汽车在整个行驶过程中的平均速度为40千米/时 D、汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少9. 如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( )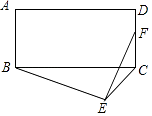 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 化简 + = .11. 关于x的正比例函数y=(m+2)x,若y随x的增大而增大,则m的取值范围是 .
12. 在平面直角坐标系中,点(﹣2,3)到原点的距离是 .
13. 如图,平行四边形ABCD的对角线相交于点O,BC=7,BD=10,AC=6,则△AOD的周长是 . 14. 如图,把一张矩形的纸沿对角线BD折叠,若AD=8,CE=3,则DE= .
14. 如图,把一张矩形的纸沿对角线BD折叠,若AD=8,CE=3,则DE= .
三、解答题
-
15. 计算:(1)、3 ﹣2 +3(2)、( ﹣1)2+ .16. 如图,为修铁路需凿通隧道AC,现测量出∠ACB=90°,AB=5km,BC=4km,若每天凿隧道0.2km,问几天才能把隧道AC凿通?
 17. 已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
17. 已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F. (1)、求证:△AEB≌△CFD;(2)、连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
(1)、求证:△AEB≌△CFD;(2)、连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形. 18. 如图,在▱ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
18. 如图,在▱ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF, (1)、求证:四边形ABCD为矩形;(2)、过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.19. 某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)
(1)、求证:四边形ABCD为矩形;(2)、过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.19. 某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)
请根据图中提供的信息,回答下列问题:
(1)、α= , 并写出该扇形所对圆心角的度数为 , 请补全条形图 .(2)、在这次抽样调查中,众数和中位数分别是多少?(3)、如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?20. 已知直线y=kx+b经过点A(5,0),B(1,4). (1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集.21. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集.21. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: (1)、写出A、B两地之间的距离;(2)、求出点M的坐标,并解释该点坐标所表示的实际意义;(3)、若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.22. 端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.(1)、请求出两种口味的粽子每盒的价格;(2)、设买大枣粽子x盒,买水果共用了w元.
(1)、写出A、B两地之间的距离;(2)、求出点M的坐标,并解释该点坐标所表示的实际意义;(3)、若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.22. 端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.(1)、请求出两种口味的粽子每盒的价格;(2)、设买大枣粽子x盒,买水果共用了w元.①请求出w关于x的函数关系式;
②求出购买两种粽子的可能方案,并说明哪一种方案使购买水果的钱数最多.