河北省唐山市路北区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-04 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 在函数y= x−1 中，x的取值范围是（   ）
    A、x≥1 B、x≤1 C、x≠1 D、x＜0

    查看试题解析

  • 2. 如图图形中，既是中心对称图形又是轴对称图形的是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 3. 一个正多边形的边长为2，每个内角为135°，则这个多边形的周长是（   ）

    A、8 B、12 C、16 D、18

    查看试题解析

  • 4. 关于一次函数y=2x﹣1的图象，下列说法正确的是（   ）

    A、图象经过第一、二、三象限 B、图象经过第一、三、四象限 C、图象经过第一、二、四象限 D、图象经过第二、三、四象限

    查看试题解析

  • 5. 一个不透明的布袋里装有5个只有颜色不同的球，其中2个红球，3个白球，从布袋中随机摸出一个球，摸出红球的概率是（   ）
    A、12 B、23 C、25 D、35

    查看试题解析

  • 6. 矩形、菱形、正方形都具有的性质是（    ）．

    A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角

    查看试题解析

  • 7. 某同学对甲、乙、丙、丁四个市场五月份每天的白菜价格进行调查，计算后发现这四个市场的平均价格相同，方差分别为s甲2=10.1，s乙2=8.5，s丙2=6.5，s丁2=2.6，则五月份白菜价格最稳定的市场是（   ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 8. 一次函数y=kx+b的图象如图所示，当y＞3时，x的取值范围是（   ）

    A、x＜0 B、x＞0 C、x＜2 D、x＞2．

    查看试题解析

  • 9. 若把一次函数y=2x﹣3的图象向上平移3个单位长度，得到图象对应的函数解析式为（   ）
    A、y=2x B、y=2x﹣6 C、y=4x﹣3 D、y=﹣x﹣3

    查看试题解析

  • 10. 园林队在某公园进行绿化，中间休息了一段时间．已知绿化面积S（单位：平方米）与工作时间t（单位：小时）的函数关系的图象如图，则休息后园林队每小时绿化面积为（   ）

    A、40平方米 B、50平方米 C、80平方米 D、100平方米

    查看试题解析

  • 11. 如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD．若BD=1，则AC的长是（   ）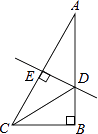

    A、2 3 B、2 C、4 3 D、4

    查看试题解析

  • 12. 如图，在Rt△ABD中，∠BDA=90°，AD=BD，点E在AD上，连接BE，将△BED绕点D顺时针旋转90°，得到△ACD，若∠BED=65°，则∠ACE的度数为（   ）

    A、15° B、20° C、25° D、30°

    查看试题解析

  • 13. Rt△ABC中，斜边BC=2，则AB2+AC2+BC2的值为（　　）

    A、8 B、4 C、6 D、无法计算

    查看试题解析

  • 14. 如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：（1）AE=BF；（2）AE⊥BF；（3）AO=OE；（4）S△AOB=S四边形DEOF中正确的有（   ）

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

二、填空题

  • 15. 若函数y=（2m+6）x+（1﹣m）是正比例函数，则m的值是 ．

    查看试题解析

  • 16. 已知一次函数的图象与直线y=﹣x+1平行，且过点（8，2），则此一次函数的解析式为 ．

    查看试题解析

  • 17. 如图，矩形ABCD的长和宽分别为6和4，E、F、G、H依次是矩形ABCD各边的中点，则四边形EFGH的周长等于 ．

    查看试题解析

  • 18. 如图，在正方形ABCD中，点D的坐标为（0，1），点A的坐标是（﹣2，2），则点B的坐标为 ．

    查看试题解析

三、解答题

  • 19. 已知y是x的一次函数，当x=3时，y=1；当x=﹣2时，y=﹣4，求此一次函数的解析式．

    查看试题解析

  • 20. 如图，已知AC⊥BC，垂足为C，AC=4，BC=3 3 ，将线段AC绕点A按逆时针方向旋转60°，得到线段AD，连接DC，DB．

    (1)、线段DC=；
    (2)、求线段DB的长度．

    查看试题解析

  • 21. 如图所示网格是由边长为1的小正方形组成，点A，B，C位置如图所示，在网格中确定点D，使以A，B，C，D为顶点的四边形的所有内角都相等．

    (1)、确定点D的位置并画出以A，B，C，D为顶点的四边形；
    (2)、直接写出（1）中所画出的四边形的周长和面积．

    查看试题解析

  • 22. 老师想知道某校学生每天上学路上要花多少时间，于是随机选取30名同学每天来校的大致时间（单位：分钟）进行统计，统计表如下：

    时间

    5

    10

    15

    20

    25

    30

    35

    45

    人数

    3

    3

    6

    12

    2

    2

    1

    1

    (1)、写出这组数据的中位数和众数；

    (2)、求这30名同学每天上学的平均时间．

    查看试题解析

  • 23. “阳光体育”运动关乎每个学生未来的幸福生活，今年五月，我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛，要求每个班选2﹣3名选手参赛，现将80名选手比赛成绩（单位：次/分钟）进行统计．绘制成频数分布直方图，如图所示．

    (1)、图中a值为 ．
    (2)、将跳绳次数在160～190的选手依次记为A1、A2、…An ， 从中随机抽取两名选手作经验交流，请用树状或列表法求恰好抽取到的选手A1和A2的概率．

    查看试题解析

  • 24. 如图，▱ABCD的对角线AC、BD相交于点O，AE=CF．

    (1)、求证：△BOE≌△DOF；
    (2)、连接DE、BF，若BD⊥EF，试探究四边形EBDF的形状，并对结论给予证明．

    查看试题解析

  • 25. 新农村社区改造中，有一部分楼盘要对外销售，某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2 ， 从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2 ．

    若购买者一次性付清所有房款，开发商有两种优惠方案：

    方案一：降价8%，另外每套楼房赠送a元装修基金；

    方案二：降价10%，没有其他赠送．

    (1)、请写出售价y（元/米2）与楼层x（1≤x≤23，x取整数）之间的函数关系式；
    (2)、老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算．

    查看试题解析

  • 26. 完成题目：

    (1)、

    如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形，并证明：BE=CD；（尺规作图，不写作法，保留作图痕迹）；


    (2)、

    如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？简单说明理由；

    (3)、

    运用（1）、（2）解答中所积累的经验和知识，完成下题：

    如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．


    查看试题解析