河北省廊坊市文安县2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-04 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{2} \times \sqrt{3} = 6$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
2. 某班七个兴趣小组人数分别为4，4，5，x，6，6，7．已知这组数据的平均数是5，则这组数据的中位数是（　　）

A、7 B、6 C、5 D、4

查看试题解析
3. 等腰三角形的腰长为10，底长为12，则其底边上的高为( )

A、13 B、8 C、25 D、64

查看试题解析
4. 一次函数y=2x+4交y轴于点A，则点A的坐标为（）

A、（0，4） B、（4，0） C、（﹣2，0） D、（0，﹣2）

查看试题解析
5.
一次函数y=kx+b的图象如图所示，则k、b的值为（）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
6. 如图，在平行四边形ABCD中，连接对角线AC、BD，图中的全等三角形的对数（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
7. 下列命题中：
①两条对角线互相平分且相等的四边形是正方形；
②菱形的一条对角线平分一组对角；
③顺次连结四边形各边中点所得的四边形是平行四边形；
④两条对角线互相平分的四边形是矩形；
⑤平行四边形对角线相等．
真命题的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为（）

A、2.4cm B、4.8cm C、5cm D、9.6cm

查看试题解析
9. 甲乙两人在跳远练习中，6次成绩分别为（单位：米）：
甲：3.8 3.8 3.9 3.9 4.0 4.0；乙：3.8 3.9 3.9 3.9 3.9 4.0．
则这次跳远练习中，甲乙两人成绩方差的大小关系是（）

A、 $s_{甲}^{2}$ ＞ $s_{乙}^{2}$ B、 $s_{甲}^{2}$ ＜ $s_{乙}^{2}$ C、 $s_{甲}^{2}$ = $s_{乙}^{2}$ D、无法确定

查看试题解析
10. 从某市5000名初一学生中，随机抽取100名学生，测得他们的身高数据，得到一个样本，则这个样本数据的平均数、中位数、众数、方差四个统计量中，服装厂最感兴趣的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
11. 匀速地向如图的容器内注水，最后把容器注满，在注水过程中，水面的高度h随时间t的变化而变化，变化规律为一折线，下列图象（草图）正确的是（）

A、 B、 C、 D、

查看试题解析
12. 已知正比例函数y=（k+5）x，且y随x的增大而减小，则k的取值范围是（　　）

A、k＞5 B、k＜5 C、k＞﹣5 D、k＜﹣5

查看试题解析
13. 直线l的解析式是y=kx+2，其中k是不等式组 $\{\begin{matrix} 3 k + 4 < 0 \\ k + 9 < 0 \end{matrix}$ 的解，则直线l的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
14. 如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x、y的二元一次方程组 ${\begin{matrix} y = a x + b \\ y = k x \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ B、 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = - 3 \\ y = 1 \end{matrix}$ D、 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$

查看试题解析
15. 如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为（）cm² ．

A、4 B、8 C、12 D、16

查看试题解析
16. 如图，点O（0，0），A（0，1）是正方形OAA₁B的两个顶点，以OA₁对角线为边作正方形OA₁A₂B₁ ，再以正方形的对角线OA₂作正方形OA₁A₂B₁ ， …，依此规律，则点A₈的坐标是（）

A、（﹣8，0） B、（0，8） C、（0，8 $\sqrt{2}$ ） D、（0，16）

查看试题解析

二、填空题

17. 计算： $\sqrt{8} + \sqrt{18}$ = ．

查看试题解析
18. 如图：阴影部分（阴影部分为正方形）的面积是．

查看试题解析
19. 如图，在平行四边形ABCD中，AD=5，AB=3，BE平分∠ABC，则DE= ．

查看试题解析
20. 如图，在▱ABCD中，对角线AC、BD相交于点O，如果AC=14，BD=8，AB=x，那么x的取值范围是．

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{18}$ ﹣ $\frac{2}{\sqrt{2}}$ ﹣ $\frac{\sqrt{8}}{2}$ +（ $\sqrt{5}$ +1）⁰

(2)、（ $\sqrt{a}$ + $\sqrt{b}$ ）²﹣（ $\sqrt{a}$ ﹣ $\sqrt{b}$ ）² ．

查看试题解析
22. 一个零件的形状如图所示，工人师傅按规定做得AB=3，BC=4，AC=5，CD=12，AD=13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？

查看试题解析
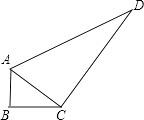23. 如图所示为某汽车行驶的路程S（km）与时间t（min）的函数关系图，观察图中所提供的信息解答下列问题：

(1)、汽车在前9分钟内的平均速度是多少？

(2)、汽车中途停了多长时间？

(3)、当16≤t≤30时，求S与t的函数关系式？

查看试题解析
24. 某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答系列问题：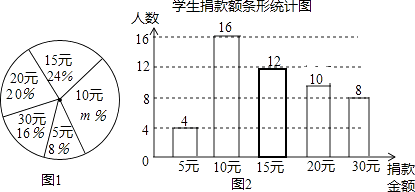

(1)、本次接受随机抽样调查的学生人数为人，图1中m的值是．

(2)、求本次调查获取的样本数据的平均数、众数和中位数；

(3)、根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

查看试题解析
25. 某校实行学案式教学，需印制若干份数学学案，印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示：

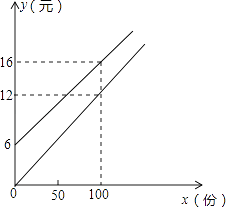(1)、填空：甲种收费的函数关系式是．
乙种收费的函数关系式是．

(2)、该校某年级每次需印制100～450（含100和450）份学案，选择哪种印刷方式较合算？

查看试题解析
26. 如图，直角梯形ABCD中，AD∥BC，AB= $4 \sqrt{2}$ cm，AD=24cm，BC=26cm，∠B=90°，动点P从A开始沿AD边向D以1cm/s的速度运动，动点Q从点C开始沿CB以3cm/s的速度向点B运动．P、Q同时出发，当其中一点到达顶点时，另一点也随之停止运动，设运动时间为ts，问：

(1)、t=时，四边形PQCD是平行四边形．

(2)、是否存在一个t值，使PQ把梯形ABCD分成面积相等的两部分？若存在请求出t的值．

(3)、当t为何值时，四边形PQCD为等腰梯形．

(4)、连接DQ，是否存在t值使△CDQ为等腰三角形？若存在请直接写出t的值．

查看试题解析