安徽省合肥市瑶海区2019年中考数学二模考试试卷
试卷更新日期：2020-04-03 类型：中考模拟
一、单选题
-
1. 下列各数中，比0小的是（ ）A、 B、﹣（﹣1） C、|﹣1| D、﹣20192. 据报道，2019年参加全国硕士研究生考试的人数约有260万人．其中，“260万”用科学记数法可表示为（ ）A、26×108 B、2.6×106 C、0.26×108 D、260×1043. 计算（﹣3a3）2的结果是（ ）
A、﹣3a6 B、3a6 C、﹣9a6 D、9a64. 下图中的几何体的左视图是（ ）
A、
B、
C、
D、
5. 1261年，我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律，我们把这个三角形称为“杨辉三角”，请观察图中的数字排列规律，则代数式a+b+c的值为（ ）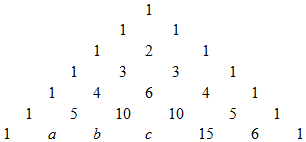
A、22 B、41 C、50 D、516. 整数n满足n﹣1＜3 ＜n，则n的值为（ ）A、7 B、8 C、9 D、107. 如图，AB为⊙O的直径，CD切⊙O于点C，交AB的延长线于点D，且CO＝CD，则∠A的度数为（ ）
A、45° B、30° C、22.5° D、37.5°8. 甲打字员计划用若干小时完成文稿的电脑输入工作，两小时后，乙打字员协助此项工作，且乙打字员文稿电脑输入的速度是甲的1.5倍，结果提前6小时完成任务，则甲打字员原计划完成此项工作的时间是（ ）A、17小时 B、14小时 C、12小时 D、10小时9. 如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A ， 图2是点P运动时，线段BP的长度y随时间x变化的函数关系图象，其中M为曲线部分的最低点下列说法错误的是（ ）
A、△ABC是等腰三角形 B、AC边上的高为4 C、△ABC的周长为16 D、△ABC的面积为10二、解答题
-
10. 抽查员随机抽取甲、乙、丙、丁四台机器生产10个乒乓球直径的长度（规格为直径40mm），整理的平均数（单位：mm）分别为39.96、40.05、39.96、40.05；方差（单位：mm2）分别为：0.36、1.12、0.20、0.5．这四台机器生产的乒乓球既标准又稳定的是（ ）A、甲 B、乙 C、丙 D、丁11. 先化简，再求值： ，其中x+y＝﹣3．12. 互联网给生活带来极大的方便据报道，2016底全球支付宝用户数为4.5亿，2018年底达到9亿．
（参考数据： ≈1.414）
(1)、求平均每年增长率；(2)、据此速度，2020底全球支付宝用户数是否会超过17亿？请说明理由．13. 在边长为1的正方形网格中建立如图所示的平面直角坐标系，点A、B、C的坐标分别为（2，1）（5，0）（1，0）．
(1)、求证：△OAC∽△OBA；(2)、在平面直角坐标系内找一点D（不与点B重合，使△OAD与△OAB全等，请直接写出所有可能的点D的坐标．14. 我们把满足方程x2+y2=z2的正整数的解（x、y、z）叫做勾股数，如，（3，4，5）就是一组勾股数．(1)、请你再写出两组勾股数：（6、8、10），（9、12、15）；(2)、在研究直角三角形的勾股数时，古希腊的哲学家柏拉图曾指出：如果n表示大于1的整数，x=2n，y=n2﹣1，z=n2+1，那么以x，y，z为三边的三角形为直径三角形（即x，y，z为勾股数），请你加以证明．15. 为开发大西北，某工程队承接高铁修筑任务，在山坡处需要修建隧道，为了测量隧道的长度，工程队用无人机在距地面高度为500米的C处测得山坡南北两端A、B的俯角分别为∠DCA＝45°、∠DCB＝30°（已知A、B、C三点在同一平面上），求隧道两端A、B的距离．（参考数据： ≈1.73）
16. 如图，在平面直角坐标系xOy中，直线y＝x+1与双曲线y＝ 的一个交点为P（m，2）．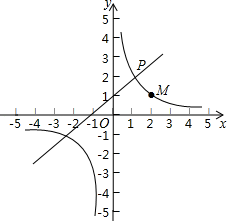
(1)、求k的值；(2)、M（ ，a），N（n，b）是双曲线上的两点，直接写出当a＞b时，n的取值范围．17. 某校为了解学生每月零用钱情况，从七、八、九年级1200名学生中随机抽取部分学生，对他们今年4月份的零用钱支出情况进行调查统计并绘制成如下统计图表：组别
零用钱支出x（单位：元）
频数（人数）
频率
节俭型
x＜10
2
0.05
10≤x＜20
4
0.10
富足型
20≤x＜30
12
30≤x＜40
m
奢侈型
40≤x＜50
n
x≥50
2
请根据图表中所给的信息，解答下列问题：
(1)、在这次调查中共随机抽取了名学生，图表中的m＝ ， n＝；(2)、请估计该校今年4月份零用钱支出在“30≤x＜40范围的学生人数；(3)、在抽样的“节俭型”学生中，有2位男生和4位女生，校团委计划从中随机抽取两人参与“映山红”的公益活动，求恰好抽中一男一女的概率．18. 我国为了实现到2020年达到全面小康社会的目标，近几年加大了扶贫工作的力度，合肥市某知名企业为了帮助某小型企业脱贫，投产一种书包，每个书包制造成本为18元，试销过程中发现，每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y＝kx+b，据统计当售价定为30元/个时，每月销售40万个，当售价定为35元/个时，每月销售30万个．(1)、请求出k、b的值．(2)、写出每月的利润w(万元)与销售单价x(元)之间的函数解析式．(3)、该小型企业在经营中，每月销售单价始终保持在25≤x≤36元之间，求该小型企业每月获得利润w(万元)的范围．19. 如图，在凸四边形ABCD中，AB＝BC＝CD，∠ABC+∠BCD＝240°．设∠ABC＝α．
(1)、利用尺规，以CD为边在四边形内部作等边△CDE．（保留作图痕迹，不需要写作法）(2)、连接AE，判断四边形ABCE的形状，并说明理由．(3)、求证：∠ADC＝ α；(4)、若CD＝6，取CD的中点F，连结AF，当∠ABC等于多少度时，AF最大，最大值为多少．（直接写出答案，不需要说明理由）．三、填空题
