安徽省阜阳市颍泉区2019年中考数学模拟考试试卷
试卷更新日期:2020-04-03 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列计算正确是( )A、m2+m3=m5 B、(m2)3=m5 C、m5 ÷m2=m3 D、2m2n•3mn2=6m2n23.
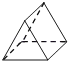
如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 2019年1月9日从相关部门获悉,2018年安徽省粮食总产801.5亿斤,总产量位居全国第4位,比去年上升1位,其中数据801.5亿用科学记数法表示为( )A、8.015×108 B、8.015×109 C、8.015×1010 D、801.5×1095. 把不等式组 的解集表示在数轴上,下列选项正确是( )A、
4. 2019年1月9日从相关部门获悉,2018年安徽省粮食总产801.5亿斤,总产量位居全国第4位,比去年上升1位,其中数据801.5亿用科学记数法表示为( )A、8.015×108 B、8.015×109 C、8.015×1010 D、801.5×1095. 把不等式组 的解集表示在数轴上,下列选项正确是( )A、 B、
B、 C、
C、 D、
D、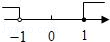 6. 如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=34°,那么∠2的度数是( )
6. 如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=34°,那么∠2的度数是( )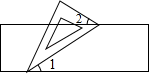 A、14° B、16° C、34° D、26°7. 每年的3月12日是我国的植树节,某学校在“爱护地球,绿化祖国”的活动中,组织了100名学生开展植树造林活动,其植树情况整理如上表,则这100名学生所植树的中位数为( )
A、14° B、16° C、34° D、26°7. 每年的3月12日是我国的植树节,某学校在“爱护地球,绿化祖国”的活动中,组织了100名学生开展植树造林活动,其植树情况整理如上表,则这100名学生所植树的中位数为( )植树棵数
4
5
6
7
9
人数
30
20
27
15
8
A、4 B、5 C、5.5 D、68. 关于x的一元二次方程2x2+4x﹣c=0有两个不相等的实数根,则实数c可能的取值为( )A、﹣5 B、﹣2 C、0 D、﹣89. 如图,在平面直角坐标系xOy中,平行四边形OABC的顶点O(0,0),B(3,2),点A在x轴的正半轴上.按以下步骤作图:①以点O为圆心,适当长度为半径作弧分别交边OA、OC于点M、N;②分别以点M、N为圆心,大于 MN的长为半径作弧,两弧在∠AOC内交于点P;③作射线OP,恰好过点B,则点A的坐标为( ) A、( ,0) B、( ,0) C、( ,0) D、(2,0)10. 如图1,矩形ABCD中,AB=4,AD=2,E、F是边AB、DC的中点,连接EF、AF,动点P从A向F运动,AP=x,y=PE+PB.图2所示的是y关于x的函数图象,点(a,b)是函数图象的最低点,则a的值为( )
A、( ,0) B、( ,0) C、( ,0) D、(2,0)10. 如图1,矩形ABCD中,AB=4,AD=2,E、F是边AB、DC的中点,连接EF、AF,动点P从A向F运动,AP=x,y=PE+PB.图2所示的是y关于x的函数图象,点(a,b)是函数图象的最低点,则a的值为( )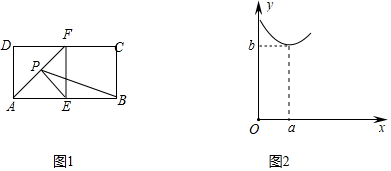 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
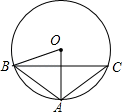
11. 9的算术平方根是 , = , ﹣ = .12. 因式分解:5a2﹣20a+20= .13. 如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC= .
 14. 如图,CD=4,∠C=90°,点B在线段CD上, ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为 .
14. 如图,CD=4,∠C=90°,点B在线段CD上, ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为 .
三、解答题
-
15. 计算:(π﹣2019)0+(1﹣sin30°)×( )﹣316. 《算法统宗》是中国古代数学名著之一,其中记载了这样的数学问题:“用绳子测水井深度,把绳子折成三折来量,井外余绳4尺;把绳子折成四折来量,井外余绳1尺,问绳长、井深各是多少尺?”.若设这个问题中的绳长为x尺,求x的值.17. 如图,在由边长为1个单位长度的小正方形组成的10×10的网格中,点A、B、C均在网格线的交点上,
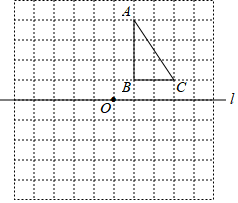 (1)、画出△ABC关于直线l对称的△A′B′C′;(2)、画出△ABC绕点O逆时针旋转90°后的△A1B1C1;(3)、在(2)的条件下,求线段BC扫过的面积(结果保留π).18. 某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32cm,∠DOB=100°,那么椅腿的长AB和篷布面的宽AD各应设计为多少cm?(结果精确到0.1cm)
(1)、画出△ABC关于直线l对称的△A′B′C′;(2)、画出△ABC绕点O逆时针旋转90°后的△A1B1C1;(3)、在(2)的条件下,求线段BC扫过的面积(结果保留π).18. 某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32cm,∠DOB=100°,那么椅腿的长AB和篷布面的宽AD各应设计为多少cm?(结果精确到0.1cm)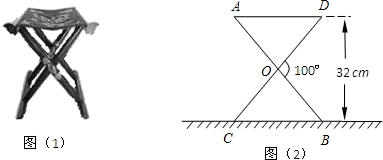 19. 观察下列等式:
19. 观察下列等式:第1个等式:
第2个等式:
第3个等式:
第4个等式:
第5个等式:
解答下列问题:
(1)、按以上规律写出第6个等式:;(2)、求a1+a2+…+a2020的值;(3)、求 的值.20. 如图,⊙O是等边△ACD的外接圆,AB是⊙O的直径,过点B作⊙O的切线BM,延长AD交BM于点E.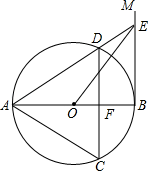 (1)、求证:CD∥BM;(2)、连接OE,若DE=4,求OE的长.21. 五一期间,育华中学组织学生参加“交通安全知识”网络测试活动该校教务处对九年级全体学生的测试成绩进行了统计,将成绩分为四个等级:优秀、良好、一般、不合格,并绘制成如下不完整的统计图.请你根据图中所给的信息解答下列问题:
(1)、求证:CD∥BM;(2)、连接OE,若DE=4,求OE的长.21. 五一期间,育华中学组织学生参加“交通安全知识”网络测试活动该校教务处对九年级全体学生的测试成绩进行了统计,将成绩分为四个等级:优秀、良好、一般、不合格,并绘制成如下不完整的统计图.请你根据图中所给的信息解答下列问题: (1)、该校九年级共有名学生,并把图1中的条形统计图补充完整.(2)、已知该市共有12000名九年级学生参加了这次“交通安全知识”网络测试,请你根据该校九年级成绩估计该市九年级学生在这次测试中成绩为优秀的人数.(3)、教务处从该校九年级成绩前5名(2男3女)的学生中随机抽取2名参加复赛,请用画树状图或列表法求出抽到“一男一女”的概率.22. 某运动专营店为某厂家代销一款学生足球比赛训练鞋(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理),当每双鞋的售价为260元时,月销售量为63双为提高经营利润,该专营店准备采取降价的方式进行促销,经市场调查发现,每月的销售量y(双)与销售单价x(元/双)之间的函数关系如图所示综合考虑各种因素,每售出双鞋需支付厂家其他费用150元.
(1)、该校九年级共有名学生,并把图1中的条形统计图补充完整.(2)、已知该市共有12000名九年级学生参加了这次“交通安全知识”网络测试,请你根据该校九年级成绩估计该市九年级学生在这次测试中成绩为优秀的人数.(3)、教务处从该校九年级成绩前5名(2男3女)的学生中随机抽取2名参加复赛,请用画树状图或列表法求出抽到“一男一女”的概率.22. 某运动专营店为某厂家代销一款学生足球比赛训练鞋(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理),当每双鞋的售价为260元时,月销售量为63双为提高经营利润,该专营店准备采取降价的方式进行促销,经市场调查发现,每月的销售量y(双)与销售单价x(元/双)之间的函数关系如图所示综合考虑各种因素,每售出双鞋需支付厂家其他费用150元.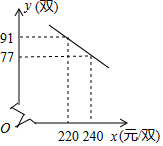 (1)、求出y与x之间的函数关系式;(2)、该运动专营店要获取最大的月利润,售价应定为每双多少元?并说明理由.(3)、2019年3月底,该专营店老板清点了一下仓库,发现该款学生足球比赛训练鞋库存650双,若根据(2)中获得最大月利润的方式进行销售,12月底能否销售完这批学生足球比赛训练鞋?请说明理由.23. 如图,正方形ABCD的边长为a,E.F分别是边AD、BC的中点,点G在CD上.且 ,DF、EG相交于点H.
(1)、求出y与x之间的函数关系式;(2)、该运动专营店要获取最大的月利润,售价应定为每双多少元?并说明理由.(3)、2019年3月底,该专营店老板清点了一下仓库,发现该款学生足球比赛训练鞋库存650双,若根据(2)中获得最大月利润的方式进行销售,12月底能否销售完这批学生足球比赛训练鞋?请说明理由.23. 如图,正方形ABCD的边长为a,E.F分别是边AD、BC的中点,点G在CD上.且 ,DF、EG相交于点H. (1)、求出 的值;(2)、求证:EG⊥DF;(3)、过点H作MN∥CD,分别交AD、BC于点M、N,点P是MN上一点,当点P在什么位置时,△PDC的周长最小,并求△PDC周长的最小值.
(1)、求出 的值;(2)、求证:EG⊥DF;(3)、过点H作MN∥CD,分别交AD、BC于点M、N,点P是MN上一点,当点P在什么位置时,△PDC的周长最小,并求△PDC周长的最小值.