安徽省2020年中考数学二模考试试卷

试卷更新日期：2020-04-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果 $2 x = 3 y$ ，那么 $\frac{x}{y}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

查看试题解析
2. 在Rt△ABC中，如果 $∠ C = 90^{0}$ ，那么 $\frac{A C}{B C}$ 表示 $∠ A$ 的（）

A、正弦 B、正切 C、余弦 D、余切

查看试题解析
3. 如图，二次函数 $y = a x^{2} + b x$ 的图象经过点A，B，C，则判断正确是（）

A、 $a > 0 ， b > 0$ B、 $a < 0 ， b < 0$ C、 $a > 0 ， b < 0$ D、 $a < 0 ， b > 0$

查看试题解析
4. 如图，如果∠BAD＝∠CAE，那么添加下列一个条件后，仍不能确定△ABC∽△ADE的是（）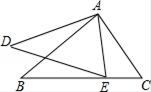

A、∠B＝∠D B、∠C＝∠AED C、 $\frac{A B}{A D}$ ＝ $\frac{D E}{B C}$ D、 $\frac{A B}{A D}$ ＝ $\frac{A C}{A E}$

查看试题解析
5. 已知向量 $\vec{a}$ 和 $\vec{b}$ 都是单位向量，那么下列等式成立的是（）

A、 $\vec{a} = \vec{b}$ B、 $\vec{a} + \vec{b} = 2$ C、 $\vec{a} - \vec{b} = 0$ D、 $| \vec{a} | = | \vec{b} |$

查看试题解析
6. 如果两圆的圆心距为2，其中一个圆的半径为3，另一个圆的半径 $r > 1$ ，那么这两个圆的位置关系不可能是（）

A、内含 B、内切 C、外离 D、相交

查看试题解析

二、填空题

7. 计算： $\frac{3}{2} \vec{a} - (\vec{a} - \frac{3}{2} \vec{b}) =$ ．

查看试题解析
8. 已知线段 $b$ 是线段 $a$ 、 $c$ 的比例中项，且 $a = 1 c m$ ， $c = 4 c m$ ，那么 $b =$ $c m$ .

查看试题解析
9. 在以 $O$ 为坐标原点的直角坐标平面内有一点 $A (4 ， 3)$ ，如果 $A O$ 与 $y$ 轴正半轴的夹角为 $α$ ，那么 $\cos α =$ .

查看试题解析
10. 如果一个正六边形的半径为 $2$ ，那么这个正六边形的周长为.

查看试题解析
11. 如果两个相似三角形的周长比为 $4 : 9$ ，那么面积比是.

查看试题解析
12. 已知线段 $A B$ 的长为 $10$ 厘米，点 $C$ 是线段 $A B$ 的黄金分割点，且 $A C > B C$ ，那么线段 $A C$ 的长为厘米.

查看试题解析
13. 已知抛物线 $y = {(x - 1)}^{2} - 4$ ，那么这条抛物线的顶点坐标为.

查看试题解析
14. 已知二次函数 $y = - x^{2} - 2$ ，那么它的图像在对称轴的部分是下降的（填“左侧”或“右侧”）.

查看试题解析
15. 已知△ABC中， ∠ACB=90° ， $A C = 6$ ， $B C = 8$ ， $G$ 为△ABC的重心，那么 $C G =$ .

查看试题解析
16. 如图，正方形DEFG的边EF在△ABC的边BC上，顶点 $D$ 、 $G$ 分别在边 $A B$ 、 $A C$ 上，已知 $B C = 6$ ，△ABC的高 $A H = 3$ ，则正方形的DEFG边长为.

查看试题解析
17. 已知Rt△ABC中， $∠ A C B = 90^{0}$ ， $A B = 10$ ， $A C = 8$ ，如果以点 $C$ 为圆心的圆与斜边 $A B$ 有唯一的公共点，那么 $⊙ C$ 的半径 $R$ 的取值范围为.

查看试题解析
18. 如果从一个四边形一边上的点到对边的视角是直角，那么称该点为直角点.例如，如图的四边形ABCD中，点 $M$ 在边CD上，连结 $A M$ 、 $B M$ ， $∠ A M B = 90^{0}$ ，则点 $M$ 为直角点.若点 $E$ 、 $F$ 分别为矩形ABCD边 $A B$ 、CD上的直角点，且 $A B = 5$ ， $B C = \sqrt{6}$ ，则线段 $E F$ 的长为.

查看试题解析

三、解答题

19. 计算： ${cos}^{2} 45^{0} - \frac{tan 30^{0}}{2 cos 30} + cot 30^{0} \cdot sin 60^{0}$ ．

查看试题解析
20. 如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，且DE= $\frac{2}{3}$ BC．

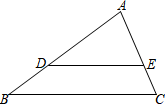(1)、如果AC=6，求AE的长；

(2)、设 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，求向量 $\vec{D E}$ （用向量 $\vec{a}$ 、 $\vec{b}$ 表示）．

查看试题解析
21. 已知：如图，AO是 $⊙ O$ 的半径，AC为 $⊙ O$ 的弦，点F为 $\overset{⌢}{A C}$ 的中点，OF交AC于点E ， AC=8，EF=2．

(1)、求AO的长；

(2)、过点C作CD⊥AO ，交AO延长线于点D ，求sin∠ACD的值．

查看试题解析
22. 安装在屋顶的太阳能热水器的横截面示意图如图所示 $.$ 已知集热管AE与支架BF所在直线相交于水箱横截面 $⊙ O$ 的圆心O ， $⊙ O$ 的半径为 $0.2$ 米，AO与屋面AB的夹角为 $32^{\circ}$ ，与铅垂线OD的夹角为 $40^{\circ}$ ， $B F ⊥ A B$ ，垂足为B ， $O D ⊥ A D$ ，垂足为D ， $A B = 2$ 米．

(1)、求支架BF的长；

(2)、求屋面AB的坡度 $.$ （参考数据： $tan 18^{\circ} \approx \frac{1}{3}$ ， $tan 32^{\circ} \approx \frac{31}{50}$ ， $tan 40^{\circ} \approx \frac{21}{25}$ ）

查看试题解析
23. 如图，△ABC中，D是BC上一点，E是AC上一点，点G在BE上，联结DG并延长交AE于点F ， ∠BGD=∠BAD=∠C ．

(1)、求证： $B D \cdot B C = B G \cdot B E$ ；

(2)、如果∠BAC=90°，求证：AG⊥BE ．

查看试题解析
24. 如图，在平面直角坐标系xOy中，二次函数 $y = a x^{2} + b x + 6$ （a、b都是常数，且a<0）的图像与x轴交于点 $A (- 2 ， 0)$ 、 $B (6 ， 0)$ ，顶点为点C.

(1)、求这个二次函数的解析式及点C的坐标；

(2)、过点B的直线 $y = - \frac{1}{2} x + 3$ 交抛物线的对称轴于点D ，联结BC ，求∠CBD的余切值；

(3)、点P为抛物线上一个动点，当∠PBA=∠CBD时，求点P的坐标.

查看试题解析
25. 如图，在 $Δ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ ， $A D ⊥ B C$ ，垂足为 $D$ ，点 $P$ 是边 $A B$ 上的一个动点，过点 $P$ 作 $P F ∥ A C$ 交线段 $B D$ 于点 $F$ ，作 $P G ⊥ A B$ 交 $A D$ 于点 $E$ ，交线段 $C D$ 于点 $G$ ，设 $B P = x$ ．

(1)、用含 $x$ 的代数式表示线段 $D G$ 的长；

(2)、设 $Δ D E F$ 的面积为 $y$ ，求 $y$ 与 $x$ 之间的函数关系式，并写出定义域；

(3)、 $Δ P E F$ 能否为直角三角形？如果能，求出 $B P$ 的长；如果不能，请说明理由．

查看试题解析