安徽省合肥市2019年中考数学模拟考试试卷
试卷更新日期:2020-04-03 类型:中考模拟
一、单选题
-
1. 二次函数y=x2+2x+3的图象的开口方向为( )
A、向上 B、向下 C、向左 D、向右2. 如图,在△ABC中,∠A=90°.若AB=12,AC=5,则cosC的值为( )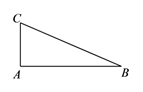 A、 B、 C、 D、3. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高.如果BD=4,CD=6,那么BC:AC是( )
A、 B、 C、 D、3. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高.如果BD=4,CD=6,那么BC:AC是( ) A、3:2 B、2:3 C、 D、 .4. 下列四个立体图形中,其主视图是轴对称图形但不是中心对称图形的是( )A、
A、3:2 B、2:3 C、 D、 .4. 下列四个立体图形中,其主视图是轴对称图形但不是中心对称图形的是( )A、 B、
B、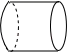 C、
C、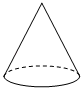 D、
D、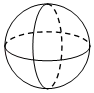 5. 若点A(x1 , 2)、B(x2 , 5)都在反比例函数y= 的图象上,则一定正确是( )A、x1<x2<0 B、x1<0<x2 C、x2<x1<0 D、x2<0<x16. 如图,四边形 内接于 ,若 ,则 ( )
5. 若点A(x1 , 2)、B(x2 , 5)都在反比例函数y= 的图象上,则一定正确是( )A、x1<x2<0 B、x1<0<x2 C、x2<x1<0 D、x2<0<x16. 如图,四边形 内接于 ,若 ,则 ( ) A、 B、 C、 D、7. 如图,AB是⊙O的直径,CD是⊙O的弦. 若∠BAD=24°, 则 的度数为( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,CD是⊙O的弦. 若∠BAD=24°, 则 的度数为( ) A、24° B、56° C、66° D、76°8. 如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m , 宽OC是4m . 按照图中所示的平面直角坐标系,抛物线可以用y=﹣ x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m . 那么两排灯的水平距离最小是( )
A、24° B、56° C、66° D、76°8. 如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m , 宽OC是4m . 按照图中所示的平面直角坐标系,抛物线可以用y=﹣ x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m . 那么两排灯的水平距离最小是( ) A、2m B、4m C、 m D、 m9. 如图,正方形ABCD的边长为2,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A、2m B、4m C、 m D、 m9. 如图,正方形ABCD的边长为2,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )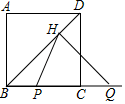 A、
A、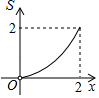 B、
B、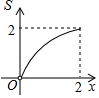 C、
C、 D、
D、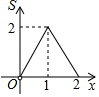 10. 如图,在Rt△ABC中,∠C=90°,AD=BD,CE=2BE.过B作BF∥CD交AE的延长线为F.当BF=1时,AB的长为( )
10. 如图,在Rt△ABC中,∠C=90°,AD=BD,CE=2BE.过B作BF∥CD交AE的延长线为F.当BF=1时,AB的长为( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
11. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是 .12. 一个不透明布袋里共有5个球(只有颜色不同),其中3个是黑球,2个是白球,从中随机摸出一个球,记下颜色后放回、搅匀,再随机摸出一个球,则两次摸出的球是一黑一白的概率是.13. 已知点P在反比例函数y= 图象的第二象限上,PM⊥x轴,PN⊥y轴,M、N为垂足,矩形PMON的面积为2,则k= .14. 如图,⊙O是△ABC的外接圆,∠BAC=60°,OD⊥BC于点D , 若BC= ,则劣弧BC的长为(结果保留π)

三、解答题
-
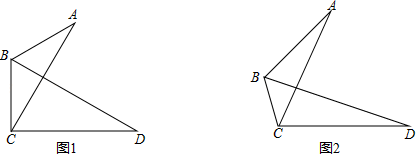
15. 计算: ﹣(﹣2)0+|1﹣ |+2cos30°.16. 如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂 长为 灯翠 长为 ,底座 厚度为 根据使用习惯,灯臂 的倾斜角 固定为 ,
 (1)、当 转动到与桌面平行时,求点 到桌面的距离;(2)、在使用过程中发现,当 转到至 时,光线效果最好,求此时灯罩顶端 到桌面的高度(参考数据: ,结果精确到个位).17. 如图所示,在边长为1个单位长度的小正方形组成的网格中, 的顶点A、B、C在格点(网格线的交点)上.
(1)、当 转动到与桌面平行时,求点 到桌面的距离;(2)、在使用过程中发现,当 转到至 时,光线效果最好,求此时灯罩顶端 到桌面的高度(参考数据: ,结果精确到个位).17. 如图所示,在边长为1个单位长度的小正方形组成的网格中, 的顶点A、B、C在格点(网格线的交点)上. (1)、将 绕点B逆时针旋转 ,得到 ,画出 ;(2)、以点A为位似中心放大 ,得到 ,使放大前后的三角形面积之比为1:4,请你在网格内画出 .18. 如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)、将 绕点B逆时针旋转 ,得到 ,画出 ;(2)、以点A为位似中心放大 ,得到 ,使放大前后的三角形面积之比为1:4,请你在网格内画出 .18. 如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘. (1)、转动甲转盘,指针指向的数字小于3的概率是;(2)、同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.19. 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)、转动甲转盘,指针指向的数字小于3的概率是;(2)、同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.19. 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4. (1)、求反比例函数解析式;(2)、求点C的坐标.20. 如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)、求反比例函数解析式;(2)、求点C的坐标.20. 如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. (1)、求证:DE是⊙O的切线.(2)、求DE的长.21. 某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)、求证:DE是⊙O的切线.(2)、求DE的长.21. 某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)、求y与x之间的函数关系式;(2)、当售价定为多少元时,每天的销售利润最大?最大利润是多少?