山西省晋城市2019-2020学年高三文数第一次模拟试卷
试卷更新日期:2020-04-03 类型:高考模拟
一、选择题
-
1. 已知复数 ,则 ( )A、1 B、2 C、 D、2. 已知集合 , ,则 ( )A、 B、 C、 D、3. 经调查,在某商场扫码支付的老年人、中年人、青年人的比例为 ,用分层抽样的方法抽取了一个容量为 的样本进行调查,其中中年人人数为9,则 ( )A、30 B、40 C、60 D、804. 已知 是正项等比数列, ,则 ( )A、 B、2 C、 D、45. 甲、乙两人近五次某项测试成绩的得分情况如图所示,则( )
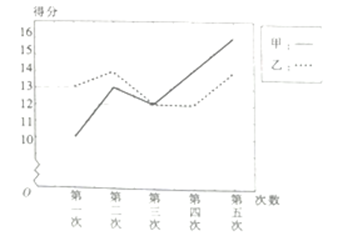 A、甲得分的平均数比乙的大 B、乙的成绩更稳定 C、甲得分的中位数比乙的大 D、甲的成绩更稳定6. 已知 是两条不同的直线, 是两个不同的平面,且 , ,则下列命题中为真命题的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 函数 在 的图像大致为( )A、
A、甲得分的平均数比乙的大 B、乙的成绩更稳定 C、甲得分的中位数比乙的大 D、甲的成绩更稳定6. 已知 是两条不同的直线, 是两个不同的平面,且 , ,则下列命题中为真命题的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 函数 在 的图像大致为( )A、 B、
B、 C、
C、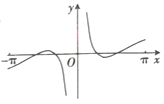 D、
D、 8. 斜率为 的直线 过抛物线 的焦点 ,若 与圆 相切,则 ( )A、12 B、8 C、10 D、69. 将函数 的图像向右平移 个单位长度,再将图像上各点的横坐标伸长到原来的6倍(纵坐标不变),得到函数 的图像,若 为奇函数,则 的最小值为( )A、 B、 C、 D、10. 已知双曲线 的两个顶点分别为 , , 的坐标分别为 , ,且四边形 的面积为 ,四边形 内切圆的周长为 ,则 的方程为( )A、 B、 或 C、 D、 或11. 如图,在长方体 中, , ,异面直线 与 所成角的余弦值为 ,则该长方体外接球的表面积为( )
8. 斜率为 的直线 过抛物线 的焦点 ,若 与圆 相切,则 ( )A、12 B、8 C、10 D、69. 将函数 的图像向右平移 个单位长度,再将图像上各点的横坐标伸长到原来的6倍(纵坐标不变),得到函数 的图像,若 为奇函数,则 的最小值为( )A、 B、 C、 D、10. 已知双曲线 的两个顶点分别为 , , 的坐标分别为 , ,且四边形 的面积为 ,四边形 内切圆的周长为 ,则 的方程为( )A、 B、 或 C、 D、 或11. 如图,在长方体 中, , ,异面直线 与 所成角的余弦值为 ,则该长方体外接球的表面积为( ) A、 B、 C、 D、12. 设函数 ,则不等式 的解集是( )A、 B、 C、 D、
A、 B、 C、 D、12. 设函数 ,则不等式 的解集是( )A、 B、 C、 D、二、填空题
-
13. 设 满足约束条件 ,则 的最小值为.14. 已知向量 , ,若 ,则 .15. 函数 的图像在点 处的切线垂直于直线 ,则 .16. 对于等差数列和等比数列,我国古代很早就有研究成果,北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”,就是关于高阶等差级数求和的问题.现有一货物堆,从上向下查,第一层有2个货物,第二层比第一层多3个,第三层比第二层多4个,以此类推,记第 层货物的个数为 ,则数列 的通项公式 , 数列 的前 项和 .
三、解答题
-
17. 在 中,角 的对边分别为 ,且 .(1)、求 ;(2)、若 , 的面积为 ,求 的周长.18. “绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展,下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份
2014
2015
2016
2017
2018
销量(万台)
8
10
13
25
24
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车
购置新能源车
总计
男性车主
6
24
女性车主
2
总计
30
(1)、求新能源乘用车的销量 关于年份 的线性相关系数 ,并判断 与 是否线性相关;(2)、请将上述 列联表补充完整,并判断是否有 的把握认为购车车主是否购置新能源乘用车与性别有关;参考公式: , ,其中 . ,若 ,则可判断 与 线性相关.
附表:
0.10
0.05
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
19. 如图,在直四棱柱 中,底面 为梯形, , , , , ,点 在线段 上, , . (1)、证明: 平面 ;(2)、求点 到平面 的距离.20. 已知椭圆 的半焦距为 ,圆 与椭圆 有且仅有两个公共点,直线 与椭圆 只有一个公共点.(1)、求椭圆 的标准方程;(2)、已知动直线 过椭圆 的左焦点 ,且与椭圆 分别交于 两点,点 的坐标为 ,证明: 为定值.
(1)、证明: 平面 ;(2)、求点 到平面 的距离.20. 已知椭圆 的半焦距为 ,圆 与椭圆 有且仅有两个公共点,直线 与椭圆 只有一个公共点.(1)、求椭圆 的标准方程;(2)、已知动直线 过椭圆 的左焦点 ,且与椭圆 分别交于 两点,点 的坐标为 ,证明: 为定值.