浙江省义乌、金华、丽水市2020年中考数学模拟试卷1

试卷更新日期：2020-04-03 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一个选项是符合题目要求的)

1. 计算–（–12）的结果是（）

A、12 B、–12 C、 $\frac{1}{12}$ D、− $\frac{1}{12}$

查看试题解析
2. 2019年11月21日，某位华师一附中高一年级的同学测得厚德广场处的气温为3℃，当时他所在教室的气温是6℃，比3℃低6℃的温度是（）℃

A、 3 B、﹣3 C、9 D、﹣9

查看试题解析
3. 下列运算正确的是（）

A、5a-4a=a B、 $x \cdot x^{2} = x^{2}$ C、 ${(n^{2})}^{3} = n^{5}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
4. 学校在李老师家的南偏东 $30 °$ 方向，距离是500m，则李老师家在学校的（）

A、北偏东 $30 °$ 方向，相距500m处 B、北偏西 $30 °$ 方向，相距500m处 C、北偏东 $60 °$ 方向，相距500m处 D、北偏西 $60 °$ 方向，相距500m处

查看试题解析
5. 若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（）

A、1 B、2 C、3 D、8

查看试题解析
6. 若代数式 $x^{2} + 6 x + m = {(x + 3)}^{2} - 1$ ，则 $m =$ （）

A、-8 B、9 C、8 D、-9

查看试题解析
7. 如图，是一个圆锥的主视图，则这个圆锥的全面积是（）

A、12π B、15π C、21π D、24π

查看试题解析
8. 在四张质地、大小相同的卡片上，分别画有如图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是中心对称图形的概率为（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
9.
在△ABC中，a、b、c分别为角A、B、C的对边，若∠B=60°，则 $\frac{c}{a + b} + \frac{a}{c + b}$ 的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、1 D、 $\sqrt{2}$

查看试题解析
10. 如图，已知正方形ABCD的边长为6，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：① $Δ A D G ≌ Δ F D G$ ；② $G B = 2 A G$ ；③ $Δ G D E ∽ Δ B E F$ ；④ $S_{Δ B E F} = \frac{18}{5}$ 在以上4个结论中，正确的有（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分)

11. 不等式 $3 x - 6 < 0$ 的解集是.

查看试题解析
12. 如图，将下列四个图形拼成一个大长方形，再据此写出一个多项式的因式分解：.

查看试题解析
13. 已知一组数据：﹣3，﹣3，4，﹣3，x，2；若这组数据的平均数为1，则这组数据的中位数是．

查看试题解析
14. 某人沿着坡度为 $1 ： 2$ 的坡面前进了 $10 \sqrt{5}$ 米，此时他与水平地面的垂直距离为米.

查看试题解析
15. A，B两地之间有一条6000米长的直线跑道，小月和小华分别从A，B两地同时出发匀速跑步，相向而行，第一次相遇后，小月将自己的速度提高25%，并匀速跑步到达B点，到达后原地休息；小华匀速跑步到达A点后，立即调头按原速返回B点（调头时间忽略不计），两人距各自出发点的距离之和记为y（米），跑步时间记为x（分钟），已知y（米）与x（分钟）之间的关系如图所示，则小月到达B点后，再经过分钟小华回到B点.

查看试题解析
16. 如图，是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，一辆小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？；(填“是”或“否”)请简述你的理由.(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84)

查看试题解析

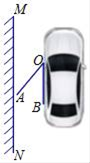
三、解答题（本大题共8小题，共66分)

17. 解方程组： ${\begin{array}{l} 2 x - y = 7 \\ x + y = - 1 \end{array}$

查看试题解析
18. 先化简，再求代数式 $\frac{x^{2} - 2 x}{x^{2} - 4} \div (x - 2 - \frac{2 x - 4}{x + 2})$ 的值，其中x＝4cos60°+3tan30°.

查看试题解析
19. 如图， $A B$ 为⊙ $O$ 的直径，过点 $C$ 的切线 $D E$ 交 $A B$ 的延长线于点 $D$ ， $A E ⊥ D C$ ，垂足为 $E$ .求证： $A C$ 平分 $∠ B A E$ .

查看试题解析
20. 某校有1500名学生，小明想了解全校学生每月课外阅读书籍的数量情况，随机抽取了部分学生，得到如统计图：

(1)、一共抽查了多少人？

(2)、每月课外阅读书籍数量是1本的学生对应的圆心角度数是多少？

(3)、估计该校全体学生每月课外阅读书籍的总量大约是多少本？

查看试题解析
21. 如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）.若反比例函数 $y_{1} = \frac{k_{1}}{x}$ （x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F.设直线EF的解析式为y₂=k₂x+b.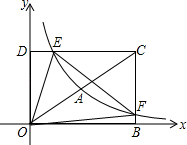

(1)、求反比例函数和直线EF的解析式；
（温馨提示：平面上有任意两点M（x₁ ， y₁）、N（x₂ ， y₂），它们连线的中点P的坐标为（ $\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2}$ ））

(2)、求△OEF的面积；

(3)、请结合图象直接写出不等式k₂x -b﹣ $\frac{k_{1}}{x}$ ＞0的解集.

查看试题解析
22. 如图，在平面直角坐标系中，点 $A (1 ， 3)$ ，点 $B (3 ， 1)$ ，点 $C (4 ， 5)$ .

(1)、画出 $Δ A B C$ 关于 $y$ 轴的对称图形 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $A$ 的对称点 $A_{1}$ 的坐标；

(2)、若点 $P$ 在 $x$ 轴上，连接 $P A$ 、 $P B$ ，则 $P A + P B$ 的最小值是；

(3)、若直线 $M N / / y$ 轴，与线段 $A B$ 、 $A C$ 分别交于点 $M$ 、 $N$ （点 $M$ 不与点 $A$ 重合），若将 $Δ A M N$ 沿直线 $M N$ 翻折，点 $A$ 的对称点为点 $A'$ ，当点 $A'$ 落在 $Δ A B C$ 的内部（包含边界）时，点 $M$ 的横坐标 $m$ 的取值范围是.

查看试题解析
23. 已知：在△ABC中，∠BAC＝90°，AB＝AC.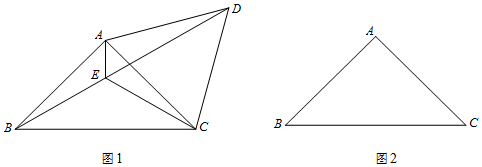

(1)、如图1，将线段AC绕点A逆时针旋转60°得到AD，连结CD、BD，∠BAC的平分线交BD于点E，
连结CE.

①求证：∠AED＝∠CED；

②用等式表示线段AE、CE、BD之间的数量关系（直接写出结果）；

(2)、在图2中，若将线段AC绕点A顺时针旋转60°得到AD，连结CD、BD，∠BAC的平分线交BD的延长线于点E，连结CE.请补全图形，并用等式表示线段AE、CE、BD之间的数量关系，并证明.

查看试题解析
24. 如图，已知抛物线y＝﹣ $\frac{1}{2} x^{2}$ +bx+c的图象经过点A(﹣1，0)和点C(0，2)，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为(m，0)，过点P作x轴的垂线l交抛物线于点Q，交直线BD于点M.

(1)、求该抛物线所表示的二次函数的表达式.

(2)、已知点F(0， $\frac{1}{2}$ )，当点P在x轴正半轴上运动时，试求m为何值时，四边形DMQF是平行四边形？

(3)、点P在线段AB运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由.

查看试题解析