浙江省义乌、金华、丽水市2020年中考数学模拟试卷2

试卷更新日期：2020-04-03 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一个选项是符合题目要求的)

1. 计算25－3×[3²＋2×(－3)]＋5的结果是（）

A、21 B、30 C、39 D、71

查看试题解析
2. 如果用表示1个立方体，用表示两个立方体叠加，用█表示三个立方体叠加，那么下图由6个立方体叠成的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 据报道，2017年11月11日淘宝网一天的销售额为1682亿元，这个数据用科学记数法表示为（）

A、1682×10⁸ B、16.82×10¹⁰ C、1.682×10¹⁰ D、1.682×10¹¹

查看试题解析
4. 如下图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中，汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：
①汽车在途中停留了0.5小时；②汽车行驶3小时后离出发地最远；③汽车共行驶了120千米；④汽车返回时的速度是80千米/小时.其中正确的说法共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列计算错误的是（）

A、a²÷a⁰•a²=a⁴ B、a²÷（a⁰•a²）=1 C、（﹣1.5）⁸÷（﹣1.5）⁷=﹣1.5 D、﹣1.5⁸÷（﹣1.5）⁷=﹣1.5

查看试题解析
6. 如果把存入3万元记作+3万元，那么支取2万元记作（）

A、+2万元 B、﹣2万元 C、﹣3万元 D、+3万元

查看试题解析
7. 设S₁=1，S₂=1+3，S₃=1+3+5，…，S_n=1+3+5+…+（2n-1），S= $\sqrt{S_{1}}$ + $\sqrt{S_{2}}$ +… $\sqrt{S_{n}}$ （其中n为正整数），当n=20时，S的值为（）

A、200 B、210 C、390 D、400

查看试题解析
8. 一个不透明的盒子中装有3个白球、9个红球，这些球除颜色外，没有任何其他区别，现从这个盒子中随机摸出一个球，摸到红球的可能性是（）

A、 $\frac{3}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
9. 在Rt△ABC中，∠C=90°，BC=a，AC=b，a+b=16，则Rt△ABC的面积S关于边长a的函数关系式为（）.

A、 $s = \frac{1}{2} a^{2} - 8 a$ B、 $s = - \frac{1}{2} a^{2} + 8 a$ C、S=a²-16a D、S=a²-16a

查看试题解析
10. 如图，在▱ABCD中，点M为CD中点，AM 与BD相交于点 N，那么S_△_{DM N}∶S_▱ABCD为（）

A、1∶12 B、1∶9 C、1∶8 D、1∶6

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分)

11. 因式分解： $b x^{2} - 2 b x + b =$ .

查看试题解析
12. 机械厂加工车间有85名工人，平均每人每天加工大齿轮16个或小齿轮10个，2个大齿轮和3个小齿轮配成一套，问，需分别安排多少名工人加工大、小齿轮，才能使每天加工的大小齿轮刚好配套？若设需安排x名工人加工大齿轮，y名工人加工小齿轮，则根据题意可得方程组.

查看试题解析
13. 已知扇形的弧长为4π，半径为8，则此扇形的圆心角为．

查看试题解析
14. 一次函数的图象过点 $(1 ， 3)$ 且与直线 $y = - 2 x + 1$ 平行，那么该函数解析式为.

查看试题解析
15. 如图，△ABC中.点D在BC边上，BD=AD=AC，E为CD的中点.若∠CAE=16°，则∠B为度.

查看试题解析
16. 如图，已知 $R t △ A B O$ 中， $∠ A O B = 90 °$ ，顶点 $A ， B$ 分别在反比例函数 $y = - \frac{5}{x} (x < 0)$ 与 $y = \frac{1}{x} (x > 0)$ 的图象上，则 $t a n ∠ A B O$ 的值为．

查看试题解析

三、解答题（本大题共8小题，共66分)

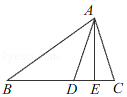
17. 如图所示，已知△ABC中，AB=AC，∠BAD=30°，AD=AE，求∠EDC的度数.

查看试题解析
18. 计算：（1﹣ $\sqrt{3}$ ）⁰+|﹣ $\sqrt{2}$ |﹣2cos45°+（ $\frac{1}{4}$ ）^﹣1

查看试题解析
19. 九（1）数学兴趣小组为了测量河对岸的古塔A、B的距离，他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点，测得∠ACB=15°，∠BCD=120°，∠ADC=30°，如图所示，求古塔A、B的距离.

查看试题解析
20. 学校为了了解我校七年级学生课外阅读的喜好，随机抽取我校七年级的部分学生进行问卷调查（每人只选一种书籍）.下图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息回答问题：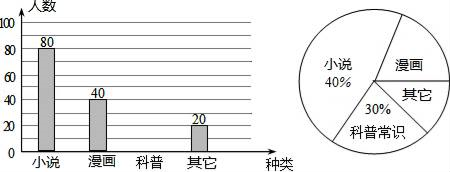

(1)、这次活动一共调查了名学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，喜欢漫画的部分所占圆心角是度；

(4)、若七年级共有学生2800人，请你估计喜欢“科普常识”的学生人数共有多少名？

查看试题解析
21. 我校为开展研究性学习，准备购买一定数量的两人学习桌和三人学习桌，若购买1张两人学习桌，1张三人学习桌需230元；若购买2张两人学习桌，3张三人学习桌需590元.

(1)、求两人学习桌和三人学习桌的单价；

(2)、学校欲投入资金不超过6600元，购买两种学习桌共60张，以至少满足137名学生的需求，有几种购买方案？并求哪种购买方案费用最低？

查看试题解析
22. 如图，公交车行驶在笔直的公路上，这条路上有A，B，C，D四个站点，每相邻两站之间的距离为5千米，从A站开往D站的车称为上行车，从D站开往A站的车称为下行车，第一班上行车、下行车分别从A站、D站同时发车，相向而行，且以后上行车、下行车每隔10分钟分别在A，D站同时发一班车，乘客只能到站点上、下车（上、下车的时间忽略不计），上行车、下行车的速度均为30千米/小时.

(1)、问第一班上行车到B站、第一班下行车到C站分别用时多少？

(2)、若第一班上行车行驶时间为t小时，第一班上行车与第一班下行车之间的距离为s千米，求s与t的函数关系式；

(3)、一乘客前往A站办事，他在B，C两站间的P处（不含B，C站），刚好遇到上行车，BP=x千米，此时，接到通知，必须在35分钟内赶到，他可选择走到B站或走到C站乘下行车前往A站.若乘客的步行速度是5千米/小时，求x满足的条件.

查看试题解析
23. 如图1，已知抛物线y=﹣x²+mx+m﹣2的顶点为A，且经过点B（3，﹣3）.

(1)、求顶点A的坐标

(2)、若P是抛物线上且位于直线OB上方的一个动点，求△OPB的面积的最大值及比时点P的坐标；

(3)、如图2，将原抛物线沿射线OA方向进行平移得到新的抛物线，新抛物线与射线OA交于C，D两点，请问：在抛物线平移的过程中，线段CD的长度是否为定值？若是，请求出这个定值；若不是，请说明理由.

查看试题解析
24. 已知：平行四边形 $A B C D$ ，对角线 $A C ⊥ A B ， A B = 9 ， A C = 12 ，$ 点P为射线BC上一点， $A P ⊥ P M$ ，（点M与点B分别在直线AP的两侧），且 $∠ P A M = ∠ C A D ，$ 联结MD.

(1)、当点M在 $▱ A B C D$ 内时，如图一，设 $B P = x ， A P = y ，$ 求 $y$ 关于 $x$ 的函数解析式.

(2)、请在图二中画出符合题意得示意图，并探究：图中是否存在与 $Δ A D M$ 相似的三角形？若存在，请写出证明过程，若不存在，请说明理由

(3)、当 $Δ A M D$ 为等腰三角形时，求 $P B$ 的长.

查看试题解析