浙江省台州市2020年中考数学模拟试卷2
试卷更新日期:2020-04-03 类型:中考模拟
一、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
-
1. 数据21、12、18、16、20、21的众数和中位数分别是( )A、21和19 B、21和17 C、20和19 D、20和182. 下列交通标志中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列命题是真命题的是( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的平行四边形是矩形 C、正方形是轴对称图形,但不是中心对称图形 D、四条边相等的四边形是萎形4. 如图,将边长相等的正方形、正五边形、正六边形纸板,按如图方式放在桌面上,则 的度数是( )
3. 下列命题是真命题的是( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的平行四边形是矩形 C、正方形是轴对称图形,但不是中心对称图形 D、四条边相等的四边形是萎形4. 如图,将边长相等的正方形、正五边形、正六边形纸板,按如图方式放在桌面上,则 的度数是( )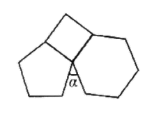 A、 B、 C、 D、5. x是最大的负整数,y是最小的正整数,则x-y的值为( )A、0 B、2 C、-2 D、±26. 甲、乙两人环湖竞走,环湖一周为 400 米,乙的速度是80 米/分,甲的速度是乙的 1 倍,且竞走开始时甲在乙前 100 米处,多少分钟后两人第一次相遇?设经过 x 分钟两人第一次相遇,所列方程为( )A、80 x+ 100= × 80 x B、80 x + 300= ×80 x C、80 x - 100= ×80 x D、80 x - 300= ×80 x7. 小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:首先画出数轴,设原点为点 ,在原点右侧 个单位长度的位置找一个点A,然后过点 作 ,且 .以点 为圆心, 为半径作弧,设与数轴右侧交点为点 ,则点 的位置在 数轴上( )
A、 B、 C、 D、5. x是最大的负整数,y是最小的正整数,则x-y的值为( )A、0 B、2 C、-2 D、±26. 甲、乙两人环湖竞走,环湖一周为 400 米,乙的速度是80 米/分,甲的速度是乙的 1 倍,且竞走开始时甲在乙前 100 米处,多少分钟后两人第一次相遇?设经过 x 分钟两人第一次相遇,所列方程为( )A、80 x+ 100= × 80 x B、80 x + 300= ×80 x C、80 x - 100= ×80 x D、80 x - 300= ×80 x7. 小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:首先画出数轴,设原点为点 ,在原点右侧 个单位长度的位置找一个点A,然后过点 作 ,且 .以点 为圆心, 为半径作弧,设与数轴右侧交点为点 ,则点 的位置在 数轴上( ) A、 和 之间 B、 和 之间 C、 和 之间 D、 和 之间8. 如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,若CD=5,AB=18,则△ABD的面积是( )
A、 和 之间 B、 和 之间 C、 和 之间 D、 和 之间8. 如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,若CD=5,AB=18,则△ABD的面积是( ) A、15 B、30 C、60 D、459. 乐陵市某中学八年级教师为鼓励学生合作学习设计了一个接力游戏——用合作的方式完成分式化简.规则是:每人只能看到前一人给的式子,并进行下一步计算,再将结果传递给下一人,最后完成化简,过程如图所示:
A、15 B、30 C、60 D、459. 乐陵市某中学八年级教师为鼓励学生合作学习设计了一个接力游戏——用合作的方式完成分式化简.规则是:每人只能看到前一人给的式子,并进行下一步计算,再将结果传递给下一人,最后完成化简,过程如图所示:
接力中,自己负责的一步出现错误的情况是( )
A、只有甲出错 B、甲和乙 C、乙和丙 D、丙和丁10. 如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( ) A、AE=EF B、AB=2DE C、△ADF和△ADE的面积相等 D、△ADE和△FDE的面积相等
A、AE=EF B、AB=2DE C、△ADF和△ADE的面积相等 D、△ADE和△FDE的面积相等二、填空题(本大题共6小题,每小题5分,共30分)
-
11. 使分式 有意义的 的取值范围是12. 若关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是 .13. 现有甲、乙两个盒子,甲盒子中有编号为4,5,6的3个球,乙盒子中有编号为7,8,9的3个球.小宇分别从这两个盒子中随机地拿出1个球,则拿出的2个球的编号之和大于12的概率为.14. 如图,在直角坐标系中,正方形OABC的顶点B的坐标为(1,4),则经过点A的双曲线的解析式为 .
 15. 定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=°.
15. 定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=°. 16. 在直角坐标系中,直线 与y轴交于点 ,按如图方式作正方形 、 、 , 、 、 在直线 上,点 、 、 在x轴上,图中阴影部分三角形的面积从左到右依次记为 、 、 、 ,则 的值为 用含n的代数式表示,n为正整数 .
16. 在直角坐标系中,直线 与y轴交于点 ,按如图方式作正方形 、 、 , 、 、 在直线 上,点 、 、 在x轴上,图中阴影部分三角形的面积从左到右依次记为 、 、 、 ,则 的值为 用含n的代数式表示,n为正整数 .
三、解答题(本大题共8小题,共80分)
-
17. 解不等式组: .
18.(1)、计算:(2)、解不等式组: ,并把不等式组的整数解写出来.19. 某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
九年级
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x)
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
八年级人数
0
0
1
11
7
1
九年级人数
1
0
0
7
10
2
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级
平均数
中位数
众数
方差
八年级
78.3
77.5
75
33.6
九年级
78
80.5
a
52.1
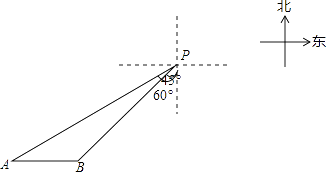
(1)、表格中a的值为;(2)、请你估计该校九年级体质健康优秀的学生人数为多少?(3)、根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)20.一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
 21. 如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证
21. 如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证 (1)、∠AHO=90°(2)、求证:CH²=AH⋅OH.22. 为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,(1)、请问工厂平均每月降低率为多少?(2)、该工厂将产品投放市场进行实销,经过调查,得到如下数据:
(1)、∠AHO=90°(2)、求证:CH²=AH⋅OH.22. 为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,(1)、请问工厂平均每月降低率为多少?(2)、该工厂将产品投放市场进行实销,经过调查,得到如下数据:销售单价 (元/件)
……
40
50
60
70
……
每天销售量 (件)
……
400
300
200
100
……
把上表中 、 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想 与 的函数关系,并求出函数关系式.
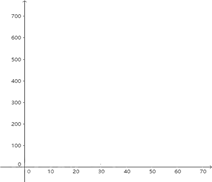 (3)、当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?23. 如图1和图2,在△ABC中,AB=13,BC=14, .
(3)、当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?23. 如图1和图2,在△ABC中,AB=13,BC=14, . (1)、探究:如图1,AH⊥BC于点H,则AH= , AC= , △ABC的面积 =.
(1)、探究:如图1,AH⊥BC于点H,则AH= , AC= , △ABC的面积 =.
(2)、拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为 =0).Ⅰ.用含x、m或n的代数式表示 及 ;
Ⅱ.求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
Ⅲ.对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
24. △ABC为等腰直角三角形,AB=AC,△ADE为等腰直角三角形,AD=AE,点D在直线BC上,连接CE. (1)、判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;(2)、若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;(3)、若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.
(1)、判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;(2)、若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;(3)、若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.