浙江省台州市2020年中考数学模拟试卷1
试卷更新日期:2020-04-03 类型:中考模拟
一、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
-
1. 2018年4月12日上午,中央军委在南海海域隆重举行新中国史上最大规模海上阅兵,展示人民海军崭新面貌,激发强国强军坚定信念.这次阅兵向世界宣示,中国海军是中国近300万平方公里海域、32000多公里海岸线的定海神针,其中32000这个数据可以用科学记数法表示为( )A、 32×104 B、3.2×105 C、3.2×104 D、3.2×1062. 某班共有学生49人,一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半,若该班男生人数为x,女生人数为y,则所列方程组正确的是( )A、 B、 C、 D、3. 若直线 与双曲线 相交于点P、Q,若点P的坐标为 ,则点Q的坐标为A、(-5,3) B、(5,-3) C、(-5,-3) D、(5,3)4. 按面划分,与圆锥为同一类几何体的是( )A、正方体 B、长方体 C、球 D、棱柱5. 下列长度的三条线段能组成三角形的是( )A、1cm, 1cm, 3cm B、1cm 2cm. 3cm C、1cm, 2cm, 2cm D、1cm, 4cm, 2cm6. 如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )
 A、6 B、8 C、10 D、127. 下列运算正确的是( )A、 B、 C、 D、8. 已知样本数据1,2,3,3,4,5,则下列说法不正确的是( )A、平均数是3 B、中位数是3 C、众数是3 D、方差是39. 如图,AB为⊙O的弦,半径OC交AB于点D,AD=DB,OC=5,OD=3,则AB的长为( )
A、6 B、8 C、10 D、127. 下列运算正确的是( )A、 B、 C、 D、8. 已知样本数据1,2,3,3,4,5,则下列说法不正确的是( )A、平均数是3 B、中位数是3 C、众数是3 D、方差是39. 如图,AB为⊙O的弦,半径OC交AB于点D,AD=DB,OC=5,OD=3,则AB的长为( )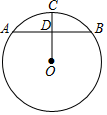 A、8 B、6 C、4 D、310. 正方形ABCD的边长为1,其面积记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2 , …按此规律继续下去,则S2019的值为( )
A、8 B、6 C、4 D、310. 正方形ABCD的边长为1,其面积记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2 , …按此规律继续下去,则S2019的值为( )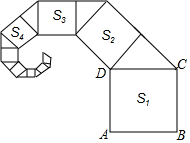 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题5分,共30分)
-
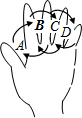
11. 如果 的算术平方根是m,-64的立方根是n,那么m-n=.12. 分解因式:﹣ a2+2a﹣2= .13. 有10个杯子,其中一等品7个,二等品3个,任意取一个杯子,是一等品的概率是。14. 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是;当字母C第201次出现时,恰好数到的数是.
 15. 如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则满足条件的AP长.
15. 如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则满足条件的AP长.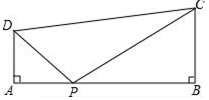 16. 如图,在⨀ 中, ,点 为 上任意一点,连接 ,则线段 之间的数量关系为.
16. 如图,在⨀ 中, ,点 为 上任意一点,连接 ,则线段 之间的数量关系为.
三、解答题(本大题共8小题,共80分)
-
17. 计算: +(π﹣3.14)0×|(﹣ )﹣1|﹣tan60°×(﹣1)201818. 先化简(1﹣x﹣ )÷ ,然后从﹣1,0,1,2中选取一个你认为合适的数作为x的值代入求值.
19. 如图,在Rt△ABC中, ,D是AB的中点,过D点作AB的垂线交AC于点E,若BC=6,sinA= ,求DE的长.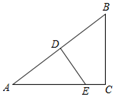
20. 小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图. 请根据图中信息,解答下列问题: (1)、这次被调查的总人数是多少?
(1)、这次被调查的总人数是多少?
(2)、试求表示A组的扇形圆心角的度数,并补全条形统计图;
(3)、如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
21. 如图,长方形ABCD表示一块草地,点E,F分别在边AB、CD上,BF∥DE,四边形EBFD是一条水泥小路,若AD=12米,AB=7米,且AE∶EB=5∶2,求草地的面积.
22. 已知一次函数y1=6x,二次函数y2=3x2+3,是否存在二次函数y3=x2+bx+c,其图象经过点(﹣4,1),且对于任意实数x的同一个值,这三个函数对应的函数值y1 , y2 , y3都有y1≤y2≤y3成立?若存在,求出函数y3的解析式;若不存在,请说明理由.
23. 如图,公交车行驶在笔直的公路上,这条路上有A,B,C,D四个站点,每相邻两站之间的距离为5千米,从A站开往D站的车称为上行车,从D站开往A站的车称为下行车,第一班上行车、下行车分别从A站、D站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在A,D站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时. (1)、问第一班上行车到B站、第一班下行车到C站分别用时多少?
(1)、问第一班上行车到B站、第一班下行车到C站分别用时多少?
(2)、若第一班上行车行驶时间为t小时,第一班上行车与第一班下行车之间的距离为s千米,求s与t的函数关系式;
(3)、一乘客前往A站办事,他在B,C两站间的P处(不含B,C站),刚好遇到上行车,BP=x千米,此时,接到通知,必须在35分钟内赶到,他可选择走到B站或走到C站乘下行车前往A站.若乘客的步行速度是5千米/小时,求x满足的条件.
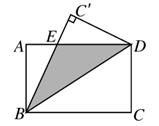
24. 小红将笔记本电脑水平放置在桌子上,显示屏 与底板 所在的水平线的夹角为 时,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架 后,电脑转到 位置(如图3),侧面示意图为图4.已知 , 于点 , .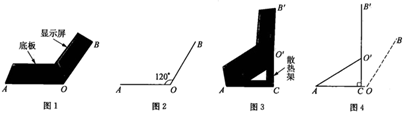 (1)、求 的度数;
(1)、求 的度数;
(2)、显示屏的顶部 比原来升高了多少?
(3)、如图4,垫入散热架后,要使显示屏 与水平线的夹角仍保持 ,则显示屏 应绕点 按顺时针方向旋转多少度?