浙江省绍兴市2020年中考数学模拟试卷2

试卷更新日期：2020-04-03 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一个选项是符合题目要求的)

1. 如果水库的水位高于正常水位 5m 记作 + 5m，那么低于正常水位 3m 应记作（）

A、+ 3 m B、- $\frac{1}{3}$ C、+ $\frac{1}{3}$ m D、- 3 m

查看试题解析
2. 为了让市民游客欢度“五一”，泉州市各地推出了许多文化旅游活动和景区优惠，旅游人气持续兴旺.从市文旅局获悉，“五一”假日全市累计接待国内外游客171.18万人次，171.18万这个数用科学记数法应表示为（）

A、1.7118×10 $^{2}$ B、0.17118×10 $^{7}$ C、1.7118×10 $^{6}$ D、171.18×10

查看试题解析
3. 小军旅行箱的密码是一个三位数，每位上的数字是0至9中的一个，由于他忘记了密码的末位数字，则小军能一次打开该旅行箱的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{9}$ C、 $\frac{1}{8}$ D、 $\frac{1}{7}$

查看试题解析
4. 下列计算结果正确的是（）

A、（a+b）²=a²+b² B、a^m•aⁿ=a^mn C、（﹣a²）³=（﹣a³）² D、（a﹣b）³•（b﹣a）²=（a﹣b）⁵

查看试题解析
5. 如图是一块带有圆形空洞和矩形空洞的小木板，则下列物体中最有可能既可以堵住圆形空洞，又可以堵住矩形空洞的是（）

A、正方体 B、球 C、圆锥 D、圆柱体

查看试题解析
6. 观察 $3^{1} - 1 = 2$ ， $3^{2} - 1 = 8$ ， $3^{3} - 1 = 26$ ， $3^{4} - 1 = 80$ ， $3^{5} - 1 = 242$ ， $3^{6} - 1 = 728$ ， $3^{7} - 1 = 2186$ ， $3^{8} - 1 = 6560$ ，…….归纳计算结果中个位数字的规律，指出 $3^{2018}$ 的个位数字是（）

A、 $2$ B、 $7$ C、 $8$ D、 $9$

查看试题解析
7. 某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y（单位：km）与时间x（单位：h）之间的关系如图所示，则下列结论正确的是（）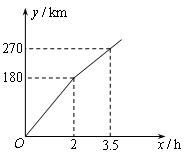

A、汽车在高速公路上的行驶速度为100km/h B、乡村公路总长为90km C、汽车在乡村公路上的行驶速度为60km/h D、该记者在出发后4.5h到达采访地

查看试题解析
8. 化简 ${(- 5)}^{2017} + 5^{2018}$ 所得的值为（）.

A、 $- 5$ B、5 C、 $2^{2016}$ D、 $4 \times 5^{2017}$

查看试题解析
9. 如图，在平面直角坐标系 $x O y$ 中，点A的坐标是 $(4 ， 2)$ ，点A关于直线 $x = 1$ 的对称点为B，若抛物线 $y = a x^{2} (a \neq 0)$ 与线段 $A B$ 恰有一个公共点，则a的取值范围是（）

A、 $a > \frac{1}{2}$ B、 $a < \frac{1}{8}$ C、 $\frac{1}{8} \leq a < \frac{1}{2}$ D、 $\frac{1}{8} \leq a \leq \frac{1}{2}$

查看试题解析
10. 在平面直角坐标系xOy中，过点A（1，6）的直线与反比例函数 $y = \frac{6}{x}$ 的图象的另一个交点为B，与x轴交于点P，若AP＝2PB，则点P的坐标是（）

A、（1，0） B、（3，0） C、（﹣1，0） D、（3，0）或（﹣1，0）

查看试题解析

二、填空题（本大题共6小题，每小题5分，共30分)

11. 分解因式： ${(a - b)}^{2} - 4 b^{2} =$ .

查看试题解析
12. 我们规定：当k，b为常数，k≠0，b≠0，k≠b时，一次函数y＝kx+b与y＝bx+k互为交换函数，例如：y＝4x+3的交换函数为y＝3x+4.一次函数y＝kx+5与它的交换函数图象的交点横坐标为.

查看试题解析
13. 如图，⊙O过△ABC的顶点A、B、C，且∠C=30°，AB= 3，则弧AB长为.

查看试题解析
14. 如图，点A的坐标为(2，0)，点B在直线y＝x上，当线段AB最短时，点B的坐标为.

查看试题解析
15. 如图，已知函数y=2x和函数 $y= \frac{k}{x}$ 的图象交于A、B两点，过点A作AE⊥x轴于点E，若△AOE的面积为4，P是坐标平面上的点，且以点B、O、E、P为顶点的四边形是平行四边形，则满足条件的P点坐标是.

查看试题解析
16. 如图，在 $Δ A B C$ 中， $B D$ 平分 $∠ A B C$ ， $B C$ 的中垂线交 $B C$ 于点 $E$ ，交 $B D$ 于点 $F$ ，连接 $C F$ ， $∠ A B D = 24^{°}$ .若 $D F = C D$ ，则 $∠ A$ 的度数为；

查看试题解析

三、解答题（本大题共8小题，共80分)

17. 解一元二次方程： $x^{2} - 2 x - 3 = 0$ .

查看试题解析
18. 小华有一个容量为8GB (1GB= 1024MB)的U盘，U盘中已经存储了一个视频文件，其余空间都用来存储照片，若每张照片占用的内存容量均相同，图片数量x (张)和剩余可用空间y (MB)的部分关系如表：

图片数量

100

150

200

400

800

剩余可用空间

5700

5550

5400

4800

3600

(1)、由上表可知，y与x之间满足(填“一次”或“二次”或“反比例”)函数的关系，求出y与x之间的关系式.

(2)、求出U盘中视频文件的占用内存容量.

查看试题解析
19. 某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵.将各类的人数绘制成扇形统计图（如图①）和条形统计图（如图②），经确认扇形统计图是正确的，而条形统计图尚有一处错误.

回答下列问题：

(1)、写出条形统计图中存在的错误，并说明理由.

(2)、写出这20名学生每人植树量的众数、中位数.

查看试题解析
20. 某无人机兴趣小组在操场上开展活动（如图），此时无人机在离地面30米的D处，无人机测得操控者A的俯角为37°，测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米，求教学楼BC的高度.（注：点A，B，C，D都在同一平面上.参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）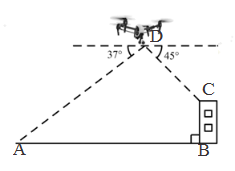

查看试题解析
21. “五一”节假期间，小亮一家到某度假村度假，小亮和他妈妈坐公交车先出发，他爸爸自驾车沿着相同的道路后出发，他爸爸到达度假村后，发现忘了东西在家里，于是立即返回家里取，取到东西后又马上驾车前往度假村，如图是他们家的距离 $s$ （ $km$ ）与小明离家的时间 $t (h)$ 的关系图，请根据图回答下列问题：

(1)、小亮和妈妈坐公交车的速度为 $km / h$ ；爸爸自驾的速度为 $km / h$ .

(2)、小亮从家到度假村期间，他离家的距离 $s (km)$ 与离家的时间 $(h)$ 的关系式为；小亮从家到度假村的路途中，当他与他爸爸相遇时，离家的距离是 $km$ .

(3)、整个运动过程中（双方全部到达会和时，视为运动结束）， $t$ 为多少时小亮和妈妈与爸爸相距 $10 km$ ？

查看试题解析
22. 如图，矩形 $A B C D$ 中， $A B = 6$ ， $A D = 8$ ，点 $P$ 从点 $A$ 出发，以每秒一个单位的速度沿 $A \to B \to C$ 的方向运动；同时点 $Q$ 从点 $B$ 出发，以每秒2个单位的速度沿 $B \to C \to D$ 的方向运动，当其中一点到达终点后两点都停止运动.设两点运动的时间为 $t$ 秒.

(1)、当 $t =$ 时，两点停止运动；

(2)、当 $t$ 为何值时， $Δ B P Q$ 是等腰三角形？

查看试题解析
23. 在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°.

(1)、延长CB至G点，使得BG=DF (如图①)，求证：△AEG≌△AEF；

(2)、若直线EF与AB，AD的延长线分别交于点M，N(如图②)，求证：EF²=ME²+NF²；

(3)、将正方形改为长与宽不相等的矩形，若其余条件不变(如图③)，请你直接写出线段EF，BE，DF之间的数量关系.

查看试题解析
24. 如图1，已知抛物线 $y = - \frac{\sqrt{3}}{3} x^{2} - \frac{2 \sqrt{3}}{3} x + \sqrt{3}$ 与x轴交于A，B两点，与y轴交于点C，顶点为D，点C’是点C关于对称轴的对称点，过点D作DG⊥x轴交x轴于点G，交线段AC于点E。

(1)、连接DC，求△DCE的周长；

(2)、如图2，点P是线段AC上方抛物线上的一点，过P作PH⊥x 轴交x轴于点H，交线段AC于点Q，当四边形PCQC’的面积最大时，在线段PH上有一动点M，在线段DG上有一动点N，在y轴上有一动点E，且满足MN⊥PH，连接AM，MN，NE，DE，求AM+MN+NE+DE的最小值；

(3)、如图3，将抛物线沿直线AC进行平移，平移过程中的点D记为D’，点C记为C’，连接D’C’所形成的直线与x轴相交于点G，请问是否存在这样的点G，使得△D’OG为等腰三角形？若存在，求出此时OG的长度，若不存在，请说明理由。

查看试题解析

图片数量	100	150	200	400	800
剩余可用空间	5700	5550	5400	4800	3600