浙江省绍兴市2020年中考数学模拟试卷1
试卷更新日期:2020-04-03 类型:中考模拟
一、选择题(本大题共10小题,每小题4分,共40分。)
-
1. 绝对值是2的数是( )A、2 B、-2 C、±2 D、2. 满足下列条件的△ABC不是直角三角形的是( )A、BC=8,AC=15,AB=17 B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:53. 据报道,我市2018年城乡居民人均可支配收入达到34534元,迈上新台阶.34534用科学记数法表示为A、 B、 C、 D、4. 如图,从上向下看几何体,得到的图形是( )
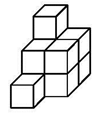 A、
A、 B、
B、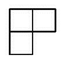 C、
C、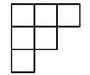 D、
D、 5. 将一抛物线向下,向右各平移 个单位得到的抛物线是 ,则该抛物线的解析式是( )A、 B、 C、 D、6. 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
5. 将一抛物线向下,向右各平移 个单位得到的抛物线是 ,则该抛物线的解析式是( )A、 B、 C、 D、6. 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )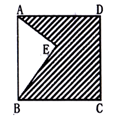 A、66 B、76 C、64 D、1007. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,某班有40名学生,达到优秀的有18人,合格的有17人,则这次体育考核中,不合格人数的频率是( )A、0.125 B、0.45 C、0.425 D、1.258. 如图,矩形 的边 , 分别在坐标轴上,且点 的坐标为 ,将矩形 沿 轴正方向平移 个单位,得到矩形 , 再以点 为旋转中心,把矩形 顺时针方向旋转 ,得到矩形 ″ ″ ″ ″ ″, ″, ″, ″ ,则点 所经过的路线为 ″的长为( )
A、66 B、76 C、64 D、1007. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,某班有40名学生,达到优秀的有18人,合格的有17人,则这次体育考核中,不合格人数的频率是( )A、0.125 B、0.45 C、0.425 D、1.258. 如图,矩形 的边 , 分别在坐标轴上,且点 的坐标为 ,将矩形 沿 轴正方向平移 个单位,得到矩形 , 再以点 为旋转中心,把矩形 顺时针方向旋转 ,得到矩形 ″ ″ ″ ″ ″, ″, ″, ″ ,则点 所经过的路线为 ″的长为( ) A、11 B、12 C、4+5 D、4+9. 若一次函数的图象与直线 平行,且与直线 交于点 ,则该一次函数的表达式为( )A、 B、 C、 D、10. 如图,平行四边形ABCD中,E是CD的延长线上一点,CD=2DE,BE与AD交于点F,若△DEF的面积为1,则平行四边形ABCD的面积为( )
A、11 B、12 C、4+5 D、4+9. 若一次函数的图象与直线 平行,且与直线 交于点 ,则该一次函数的表达式为( )A、 B、 C、 D、10. 如图,平行四边形ABCD中,E是CD的延长线上一点,CD=2DE,BE与AD交于点F,若△DEF的面积为1,则平行四边形ABCD的面积为( ) A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题(本大题共6小题,每小题5分,共30分)
-
11. 若不等式(a﹣3)x≥3﹣a的解集为x≤﹣1,则a的取值范围是.12. 在平面直角坐标系中,正比例函数 与反比例函数 的图象交于点 ,则 .13. 点 与点 关于 轴对称,则 .14. 用边长相等的正三角形与正方形两种图形铺满地面,设在一个顶点周围有x个正三角形和y个正方形,则x= , y=.15. 如图是一幅“苹果图”,第一行有1个苹果,第二行有2个,第三行有4个,第四行有8个,…….你是否发现苹果的排列规律?猜猜看,第十行有个苹果.
 16. 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG= AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=度时,∠OAG′=90°.
16. 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG= AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=度时,∠OAG′=90°.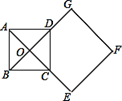
三、解答题(本大题共8小题,共80分)
-
17. 计算:
18. 某销售商准备在西安采购一批丝绸,有A型、B型两种丝绸可供选择,其进价和售价如下:A型
B型
进价 元 件
500
400
售价 元 件
800
600
若销售商购进A型、B型丝绸共50件.
(1)、求售完这50件丝绸获得总利润y元与A型丝绸的数量x件之间的函数关系式.(2)、若购进A型丝绸16件,求售完这50件丝绸获得总利润.19. 如图,在矩形 中,小聪同学利用直尺和圆规完成了如下操作: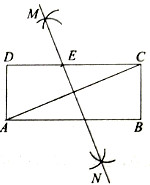
①分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ;
②作直线 ,交 于点 .
请你观察图形解答下列问题:
(1)、 与 的位置关系:直线 是线段 的线;
(2)、若 , ,求矩形的对角线 的长.20. 当太阳光线与地面成45°角时,在坡度为i=“1:2”的斜坡上的一棵树AB落在坡面上的影子AC长为5米,落在水平线上的影子CD长为3米,求这棵树的高度(参 考数据 , , ,结果保 留两个有效数字).
21. 农科所向农民推荐渝江Ⅰ号和渝江Ⅱ号两种新型良种稻谷.在田间管理和土质相同的条件下,Ⅱ号稻谷单位面积的产量比Ⅰ号稻谷低20%,但Ⅱ号稻谷的米质好,价格比Ⅰ号高.已知Ⅰ号稻谷国家的收购价是1.6元/千克.(1)、当Ⅱ号稻谷的国家收购价是多少时,在田间管理、土质和面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷的收益相同?
(2)、去年小王在土质、面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷,且进行了相同的田间管理.收获后,小王把稻谷全部卖给国家.卖给国家时,Ⅱ号稻谷的国家收购价定为2.2元/千克,Ⅰ号稻谷国家的收购价未变,这样小王卖Ⅱ号稻谷比卖Ⅰ号稻谷多收入1040元,那么小王去年卖给国家的稻谷共有多少千克?
22. 在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图.请你用所学过的有关统计的知识,回答下列问题:(图中的数字表示每一级台阶的高度(单位: )). (1)、请分别求出甲、乙两段路段每一级台阶高度的平均数.
(1)、请分别求出甲、乙两段路段每一级台阶高度的平均数.
(2)、哪段台阶路走起来更舒服?为什么?
23. 如图,已知OA是⊙O的半径,AB为⊙O的弦,过点O作OP⊥OA,交AB的延长线上一点P,OP交⊙O于点D,连接AD,BD,过点B作⊙O的切线BC交OP于点C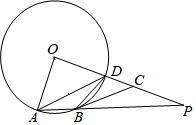 (1)、求证:∠CBP=∠ADB;
(1)、求证:∠CBP=∠ADB;
(2)、若O4=4,AB=2,求线段BP的长.
24. 如图,已知△ABC中,∠ACB=90°,AC=4,BC=3,点M、N分别是边AC、AB上的动点,连接MN,将△AMN沿MN所在直线翻折,翻折后点A的对应点为A′.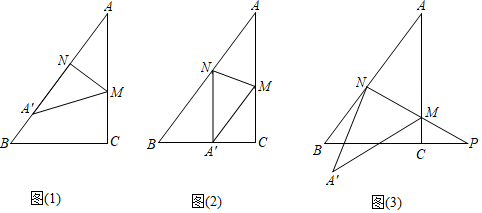 (1)、如图1,若点A′恰好落在边AB上,且AN= AC,求AM的长;(2)、如图2,若点A′恰好落在边BC上,且A′N∥AC.
(1)、如图1,若点A′恰好落在边AB上,且AN= AC,求AM的长;(2)、如图2,若点A′恰好落在边BC上,且A′N∥AC.①试判断四边形AMA′N的形状并说明理由;
②求AM、MN的长;
(3)、如图3,设线段NM、BC的延长线交于点P,当 且 时,求CP的长.