浙江省宁波市2020年中考数学模拟试卷2

试卷更新日期：2020-04-03 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题4分，共48分。)

1. 如果分式 $\frac{x}{x - 1}$ 有意义，则 $x$ 的取值范围是（）

A、 $x$ ≠0 B、 $x$ ≠1 C、 $x$ ＞1 D、 $x$ ＝1

查看试题解析
2. 用四舍五入法对3.8963取近似数，精确到0.01，得到的正确结果是（　　）

A、3.89 B、3.9 C、3.90 D、3.896

查看试题解析
3. 若 $- 2 x^{2} y^{b} + 3 x^{a} y^{3} = x^{2} y^{3}$ ，则 $| a - b |$ 等于 $($ $)$

A、 $- 1$ B、1 C、5 D、6

查看试题解析
4. 如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD=95°，∠CDE=25°，则∠DEF的度数是（）

A、110° B、115° C、120° D、125°

查看试题解析
5. 小明解方程组x+y=■的解为x=5，由于不小心滴下了两滴墨水，刚好把 ${\begin{matrix} 2 x - y = 7 \\ y = ⋆ \end{matrix}$ 两个数■和★遮住了，则这个数■和★的值为（）

A、 ${\begin{array}{l} \overset{}{\begin{array}{l} � = 8 \\ ⋆ = 3 \end{array}} \end{array}$ B、 ${\begin{array}{l} \overset{}{\begin{array}{l} � = 8 \\ ⋆ = 5 \end{array}} \end{array}$ C、 ${\begin{array}{l} \overset{}{\begin{array}{l} � = 5 \\ ⋆ = 3 \end{array}} \end{array}$ D、 ${\begin{array}{l} \overset{}{\begin{array}{l} � = 3 \\ ⋆ = 8 \end{array}} \end{array}$

查看试题解析
6. 要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（　　）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 计算m²·m⁶的结果是（）

A、m¹² B、2m⁸ C、2m¹² D、m⁸

查看试题解析
8. 若关于x的方程3m(x＋1)＋5＝m(3x－1)－5x的解是负数，则m的取值范围是（）

A、m＞－ $\frac{5}{4}$ B、m＜－ $\frac{5}{4}$ C、m＞ $\frac{5}{4}$ D、m＜ $\frac{5}{4}$

查看试题解析
9. 用5个完全相同的小正方体组合成如图所示的立体图形，它的左视图为（）

A、 B、 C、 D、

查看试题解析
10. 下列命题中，是假命题的是（）

A、任意多边形的外角和为360° B、在△ABC和△A′B′C′中，若AB＝A′B′，BC＝B′C′，∠C＝∠C′＝90°，则△ABC≌△A′B′C′ C、在一个三角形中，任意两边之差小于第三边 D、同弧所对的圆周角和圆心角相等

查看试题解析
11. 如图所示，小明从半径为 $5 c m$ 的圆形纸片中剪下 $40 %$ 圆周的一个扇形，然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠)，那么这个圆锥的高为（）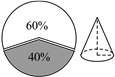

A、 $3 c m$ B、 $4 c m$ C、 $\sqrt{21} c m$ D、 $\sqrt{6} c m$

查看试题解析
12. 如图，Rt△ABC中，∠CAB=90°，在斜边CB上取点M，N（不包含C、B两点），且tanB=tanC=tan∠MAN=1，设MN=x，BM=n，CN=m，则以下结论能成立的是（）

A、m=n B、x=m+n C、x＞m+n D、x²=m²+n²

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分)

13. 分解因式： $2 a b - 4 a =$

查看试题解析
14. 在2- $\sqrt{2}$ ，- $\frac{1}{3}$ ， $0. \overset{\cdot}{3} \overset{\cdot}{6}$ ，3.14， $\frac{22}{7}$ ， $\sqrt{25}$ ，0.3131131113…（相邻两个3之间1的个数逐次加1）中，无理数是.

查看试题解析
15. 小聪需要测量学校旗杆的高度，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开4米后，发现下端刚好接触地面，则旗杆的高度为米.

查看试题解析
16. ①掷一枚使币，正面朝上；②如果 $a^{2} = b^{2}$ ，那么 $| a | = | b |$ ；③黑暗中我从一大串钥匙中随便选中一把，用它打开了门；④两条直线被第三条直线所截，同位角相等；⑤在13个人中至少有2人的出生月份相同；以上事件为“必然事件”的是；（填序号）

查看试题解析
17. 如图，在Rt△ABC中，∠ABC＝90°，AB＝6，BC＝8，P是BC边上一动点，设BP＝x，若能在AC边上找一点Q，使∠BQP＝90°，则x的范围是。

查看试题解析
18. 如图，在平面直角坐标系中，正方形 $A B C D$ 的顶点 $A$ 的坐标为 $(- 1 ， 1)$ ，点 $B$ 在 $x$ 轴正半轴上，点 $D$ 在第三象限的双曲线 $y = \frac{6}{x}$ 上，过点 $C$ 作 $C E / / x$ 轴交双曲线于点 $E$ ，连接 $B E$ ，则 $Δ B C E$ 的面积为.

查看试题解析

三、解答题（本大题共8小题，共78分)

19. 先化简，再求值：﹣2（x²﹣3y）﹣[x²﹣3（2x²﹣3y）]，其中x和y满足（x+1）²+|y+2|=0．

查看试题解析
20. 如图

(1)、如图1，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（－3，5），B（－2，1），C（－1，3）.
①画出△ABC关于x轴的对称图形△A₁B₁C₁；

②画出△A₁B₁C₁沿x轴向右平移4个单位长度后得到的△A₂B₂C₂；

③如果AC上有一点M（a，b）经过上述两次变换，写出对应A₂C₂上的点M₂的坐标。

(2)、请在图2用无刻度的直尺在图中以AB为一边画一个面积为18的长方形ABMN.（不要求写画法，但要保留画图痕迹）

查看试题解析
21. 如图，已知二次函数 $y = a x^{2} + b x + c$ 的图象过点 $A (- 1 ， 0)$ 和点 $C (0 ， 3)$ ，对称轴为直线 $x = 1$ ．

(1)、求该二次函数的关系式和顶点坐标；

(2)、结合图象，解答下列问题：
①当 $- 1 < x < 2$ 时，求函数 $y$ 的取值范围．

②当 $y < 3$ 时，求 $x$ 的取值范围．

查看试题解析
22. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利，初二数学小组在校内对“你最认可的四大新生事物”进行调查，随机调查了m人（每名学生必选一种且只能从这四种中选择一种）并将调查结果绘制成如下不完整的统计图.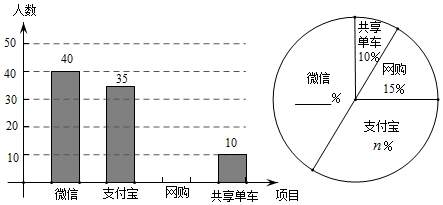

(1)、根据图中信息求出m= ， n=；

(2)、请你帮助他们将这两个统计图补全；

(3)、根据抽样调查的结果，请估算全校2000名学生中，大约有多少人最认可“微信”这一新生事物？

(4)、已知A、B两位同学都最认可“微信”，C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学，请你通过树状图或表格，求出这两位同学最认可的新生事物不一样的概率.

查看试题解析
23. 小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50min才乘上缆车，缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym.图中的折线表示小亮在整个行走过程中y与x的函数关系.

(1)、小亮行走的总路程是m，他途中休息了min，休息后继续行走的速度为m/min；

(2)、当 $50 \leq x \leq 80$ 时，求y与x的函数关系式；

(3)、当小颖到达缆车终点时，小亮离缆车终点的路程是多少？

查看试题解析
24. 如图，在梯形ABCD中， $A D ∥ B C$ ， $A B = D C = 8$ ， $B C = 12$ ， $\cos C = \frac{3}{5}$ ，点E为AB边上一点，且 $B E = 2$ .点F是BC边上的一个动点（与点B、点C不重合），点G在射线CD上，且 $∠ E F G = ∠ B$ .设BF的长为x，CG的长为y.

(1)、当点G在线段DC上时，求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、当以点B为圆心，BF长为半径的⊙B与以点C为圆心，CG长为半径的⊙C相切时，求线段BF的长；

(3)、当 $△ C F G$ 为等腰三角形时，直接写出线段BF的长.

查看试题解析
25. 如图1，直线 $y = x + 4$ 分别交x轴、y轴于A、B两点，点P是线段AB上的一动点，以P为圆心，r为半径画圆.

(1)、若点P的横坐标为﹣3，当⊙P与x轴相切时，则半径r为，此时⊙P与y轴的位置关系是.（直接写结果）

(2)、若 $r = \frac{5}{2}$ ，当⊙P与坐标轴有且只有3个公共点时，求点P的坐标.

(3)、如图2，当圆心P与A重合， $r = 2$ 时，设点C为⊙P上的一个动点，连接OC，将线段OC绕点O顺时针旋转90°，得到线段OD，连接AD，求AD长的最值并直接写出对应的点D的坐标.

查看试题解析
26. 如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、EQ.

(1)、求证：△BOQ≌△EOP；

(2)、求证：四边形BPEQ是菱形；

(3)、若AB＝6，F为AB的中点，OF+OB＝9，求PQ的长.

查看试题解析