浙江省湖州市2020年中考数学模拟试卷2
试卷更新日期:2020-04-03 类型:中考模拟
一、选择题(本大题共10小题,每小题4分,共40分。)
-
1. 12的相反数与﹣7的绝对值的和是( )A、 5 B、19 C、﹣17 D、﹣52. 计算3a3·2a2的结果是( )A、5a6 B、6a5 C、6a6 D、6a93. 下列四个几何体中,从左边看到的图形与其他三个不同的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列命题正确的个数有( )
4. 下列命题正确的个数有( )①若 x2+kx+25 是一个完全平方式,则 k 的值等于 10;②一组对边平行,一组对角相等的四边形是平行四边形;③顺次连接平行四边形的各边中点,构成的四边形是菱形;④黄金分割比的值为 ≈0.618.
A、0 个 B、1 个 C、2 个 D、3 个5. 某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:课外名著阅读量(本)
8
9
10
11
12
学生人数
3
3
4
6
4
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A、中位数是10 B、平均数是10.25 C、众数是11 D、阅读量不低于10本的同学占70%6. 如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C'处,若∠1=28°,则∠2的度数为( )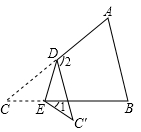 A、88° B、98° C、108° D、118°7. 若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y= (k>0)的图象上,则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y3>y1>y2 C、y3>y2>y1 D、y2>y1>y38. 如图,正六边形ABCDEF的边长为2,现将它沿AB方向平移1个单位,得到正六边形A′B′C′D′E′F′,则阴影部分A′BCDE′F′的面积是( )
A、88° B、98° C、108° D、118°7. 若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y= (k>0)的图象上,则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y3>y1>y2 C、y3>y2>y1 D、y2>y1>y38. 如图,正六边形ABCDEF的边长为2,现将它沿AB方向平移1个单位,得到正六边形A′B′C′D′E′F′,则阴影部分A′BCDE′F′的面积是( ) A、3 B、4 C、 D、29. 如图,在 中, 是 上一点, , 是 上一点, ,下列一定正确的是( )
A、3 B、4 C、 D、29. 如图,在 中, 是 上一点, , 是 上一点, ,下列一定正确的是( )
① ;② ;③ .
A、①② B、①③ C、②③ D、①②③10. 已知二次函数 的图像与x轴交于点(-2,0)、( ),且 ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6小题,每小题5分,共30分)
-
11. 若 有意义,则 =.12. 若 的值为零,则 的值是.13. 如图,菱形 的周长为 ,对角线 与 相交于点 , , ,垂足为 ,则 .
 14. 如图,将 放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
14. 如图,将 放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(I)计算 的值
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边、面积等于 的矩形,并简要说明画图方法(不要求证明)
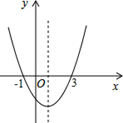
15. 已知 的三边长 , , , , , 都是整数,且 , 的最大公约数为 .点 和点 分别为 的重心和内心,且 .则 的周长为.16. 如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有.
三、解答题(本大题共8小题,共80分)
-
17. 解不等式:4﹣ ≥ ,并把解集在数轴上表示出来.18. 随着人们的生活水平的提高,家用轿车越来越多地进入家庭.小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
﹣9
﹣13
0
﹣14
﹣16
+33
+19
(1)、求出这7天的行驶路程中最多的一天比最少的一天多行驶多少千米?(2)、若每行驶100km需用汽油8升,每升汽油6.5元,计算小明家这7天的汽油费用共是多少元?19. 王老师从学校出发,到距学校 的某商场去给学生买奖品,他先步行了 后,换骑上了共享单车,到达商场时,全程总共刚好花了 .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).(1)、求王老师步行和骑共享单车的平均速度分别为多少?(2)、买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?20. 如图,已知 是 的半径,弦 , ,垂足为 ,且 . (1)、连接 ,求 的正弦值;21. 某校文体艺术节期间,举办“爱我云南,唱我云南”文艺晚会.每个班推荐一个节目参加晚会表演,参加晚会表演的节目均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,明明根据获奖情况绘制岀如图所示的两幅统计图.请你根据图中所给信息解答下列问题.
(1)、连接 ,求 的正弦值;21. 某校文体艺术节期间,举办“爱我云南,唱我云南”文艺晚会.每个班推荐一个节目参加晚会表演,参加晚会表演的节目均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,明明根据获奖情况绘制岀如图所示的两幅统计图.请你根据图中所给信息解答下列问题. (1)、二等奖的获奖人数所占的百分比是;(2)、在此次比赛中,一共有多少同学参赛?请将折线统计图补充完整.22. 如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5cm,BC=12cm,CD= cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。
(1)、二等奖的获奖人数所占的百分比是;(2)、在此次比赛中,一共有多少同学参赛?请将折线统计图补充完整.22. 如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5cm,BC=12cm,CD= cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。 (1)、当t为何值时以点P、A、D、E为顶点的四边形为直角梯形;(2)、当t为何值时以点P、A、D、E为顶点的四边形为平行四边形;(3)、点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?如能,请求出t值,如不能请说明理由。23. 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数 的图象与线段AB交于M点,且AM=BM.
(1)、当t为何值时以点P、A、D、E为顶点的四边形为直角梯形;(2)、当t为何值时以点P、A、D、E为顶点的四边形为平行四边形;(3)、点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?如能,请求出t值,如不能请说明理由。23. 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数 的图象与线段AB交于M点,且AM=BM. (1)、求点M的坐标;(2)、求直线AB的解析式.24. 已知:如图,一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)、求点M的坐标;(2)、求直线AB的解析式.24. 已知:如图,一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0) (1)、求二次函数的解析式;(2)、求四边形BDEC的面积S;(3)、在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在点P使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动的时间t的值,若不存在,请说明理由.(4)、若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由.
(1)、求二次函数的解析式;(2)、求四边形BDEC的面积S;(3)、在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在点P使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动的时间t的值,若不存在,请说明理由.(4)、若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由.