浙江省杭州市2020年中考数学模拟试卷2
试卷更新日期:2020-04-03 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,共30分。)
-
1. 下列说法错误的是( )A、有理数和无理数统称为实数; B、无限不循环小数是无理数; C、 是分数; D、 是无理数2. 下列四个立体图形中,其主视图是轴对称图形但不是中心对称图形的是( )A、
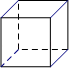 B、
B、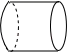 C、
C、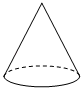 D、
D、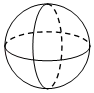 3. 如图所示的几何体的左视图是( )
3. 如图所示的几何体的左视图是( )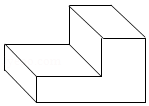 A、
A、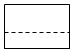 B、
B、 C、
C、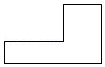 D、
D、 4. 若2n+2n+2n+2n=2,则n=( )A、﹣1 B、﹣2 C、0 D、5. 如图,一根直尺EF压在三角板 的角∠BAC上,欲使CB∥EF,则应使∠ENB的度数为( )
4. 若2n+2n+2n+2n=2,则n=( )A、﹣1 B、﹣2 C、0 D、5. 如图,一根直尺EF压在三角板 的角∠BAC上,欲使CB∥EF,则应使∠ENB的度数为( )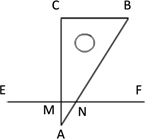 A、 B、 C、 D、6. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
A、 B、 C、 D、6. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
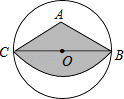
A、20 B、300 C、500 D、8007.如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2 ,则这个圆锥底面圆的半径是( )
 A、 B、 C、 D、8. 我国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”,设绳子长x尺,木条长y尺,根据题意所列方程组正确的是( )A、 B、 C、 D、9.
A、 B、 C、 D、8. 我国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”,设绳子长x尺,木条长y尺,根据题意所列方程组正确的是( )A、 B、 C、 D、9.如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
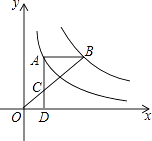 A、6 B、9 C、10 D、1210. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“
A、6 B、9 C、10 D、1210. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“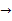 ”方向排序,如 , , ,…,根据这个规律,第 个点的横坐标为( )
”方向排序,如 , , ,…,根据这个规律,第 个点的横坐标为( )  A、44 B、45 C、46 D、47
A、44 B、45 C、46 D、47二、填空题(本大题共6小题,每小题4分,共24分)
-
11. 若代数式 和 的值相等,则x= .12. 计算 × 的值是 .13. 某校九年级科技小组,利用日晷原理,设计制造了一台简易的“日晷”,并在一个阳光明媚的日子里记录了不同时刻晷针的影长,其中10:00时的影长被墨水污染.请根据规律,判断10:00时,该晷针的影长是cm.
 14. 在平面直角坐标系中,点A(2,0),B(0,4),求点C,使以点B、O、C为顶点的三角形与△ABO全等,则点C的坐标为.15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为.
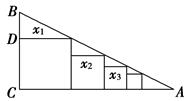
14. 在平面直角坐标系中,点A(2,0),B(0,4),求点C,使以点B、O、C为顶点的三角形与△ABO全等,则点C的坐标为.15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为. 16. 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图所示把边长分别为x1 , x2 , x3 , …,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=(用含n的式子表
16. 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图所示把边长分别为x1 , x2 , x3 , …,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=(用含n的式子表示,n≥1).
三、解答题(本大题共7小题,共66分)
-
17.(1)、计算: ;
(2)、先化简,再求值: ,其中 , .
18. 某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位: ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: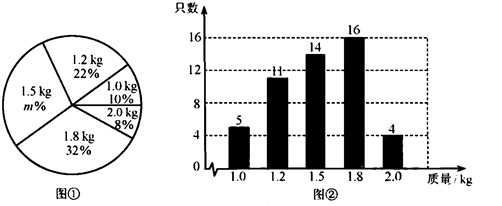
(Ⅰ)求图①中m的值;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为2.0kg的约有多少只?
19. 某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的 倍,购进数量比第一次少了30支.
(1)、求第一次每支铅笔的进价是多少元?(2)、若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
20.如图,已知BD是矩形ABCD的对角线.
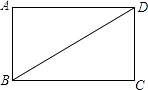 (1)、用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).(2)、连结BE,DF,问四边形BEDF是什么四边形?请说明理由.21. 如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动,动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.
(1)、用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).(2)、连结BE,DF,问四边形BEDF是什么四边形?请说明理由.21. 如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动,动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.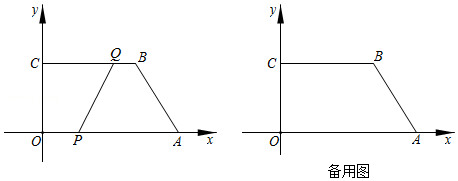 (1)、直接写出y关于t的函数解析式及t的取值范围: ,
(1)、直接写出y关于t的函数解析式及t的取值范围: ,
(2)、当PQ=3 时,求t的值,(3)、连接OB交PQ于点D,若双曲线y= (k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值,若变化,请说明理由.22.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
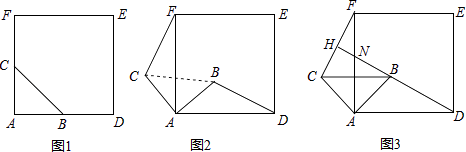 (1)、当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;(2)、当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
(1)、当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;(2)、当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.①求证:BD⊥CF;
②当AB=2,AD=3 时,求线段DH的长.
23. 如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A( ,0),在第一象限内与直线y=x交于点B(2,t).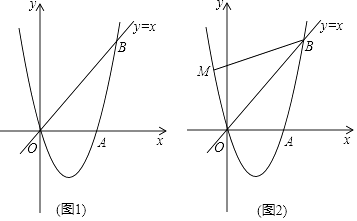 (1)、求这条抛物线的表达式;(2)、在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)、如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求这条抛物线的表达式;(2)、在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)、如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.