山东省潍坊市2020届高三数学2月模拟试卷(二)
试卷更新日期:2020-04-03 类型:高考模拟
一、单选题
-
1. 已知集合A={x|lnx<1},B={x|x2﹣x﹣2<0},则A∩B=( )A、(﹣1,2) B、(0,2) C、(﹣1,e) D、(0,e)2. 设复数z=a+bi(a,b∈R),若 ,则z=( )A、 B、 C、 D、3. 已知命题P:有的三角形是等边三角形,则( )A、¬P:有的三角形不是等边三角形 B、¬P:有的三角形是不等边三角形 C、¬P:所有的三角形都是等边三角形 D、¬P:所有的三角形都不是等边三角形4. 2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
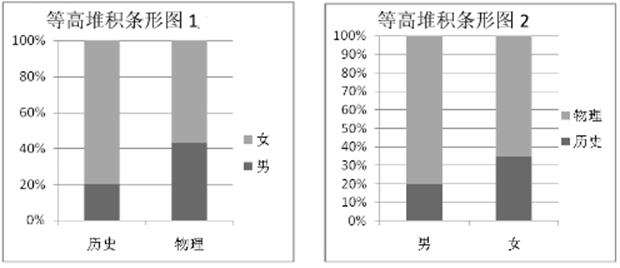 A、样本中的女生数量多于男生数量 B、样本中有学物理意愿的学生数量多于有学历史意愿的学生数量 C、样本中的男生偏爱物理 D、样本中的女生偏爱历史5. 函数 在 的图像大致为( )A、
A、样本中的女生数量多于男生数量 B、样本中有学物理意愿的学生数量多于有学历史意愿的学生数量 C、样本中的男生偏爱物理 D、样本中的女生偏爱历史5. 函数 在 的图像大致为( )A、 B、
B、 C、
C、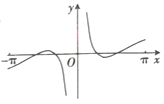 D、
D、 6. 2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式.孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( )A、 B、 C、 D、7. 已知三棱锥 的所有顶点都在球 的球面上, , ,若三棱锥 体积的最大值为2,则球 的表面积为( )A、 B、 C、 D、8. 抛物线有如下光学性质:过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 的焦点为 ,一条平行于 轴的光线从点 射出,经过抛物线上的点 反射后,再经抛物线上的另一点 射出,则 的周长为( )A、 B、 C、 D、
6. 2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式.孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( )A、 B、 C、 D、7. 已知三棱锥 的所有顶点都在球 的球面上, , ,若三棱锥 体积的最大值为2,则球 的表面积为( )A、 B、 C、 D、8. 抛物线有如下光学性质:过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 的焦点为 ,一条平行于 轴的光线从点 射出,经过抛物线上的点 反射后,再经抛物线上的另一点 射出,则 的周长为( )A、 B、 C、 D、二、多选题
-
9. 如图,正方体 的棱长为1,则下列四个命题正确的是( )
 A、直线 与平面 所成的角等于 B、点C到面 的距离为 C、两条异面直线 和 所成的角为 D、三棱柱 外接球半径为10. 若 , ,则( )A、 B、 C、 D、11. 已知函数f(x)=|sinx||cosx|,则下列说法正确的是( )A、f(x)的图象关于直线 对称 B、f(x)的周期为 C、(π,0)是f(x)的一个对称中心 D、f(x)在区间 上单调递增12. 将n2个数排成n行n列的一个数阵,如图:该数阵第一列的n个数从上到下构成以m为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列(其中m>0).已知a11=2,a13=a61+1,记这n2个数的和为S.下列结论正确的有( )
A、直线 与平面 所成的角等于 B、点C到面 的距离为 C、两条异面直线 和 所成的角为 D、三棱柱 外接球半径为10. 若 , ,则( )A、 B、 C、 D、11. 已知函数f(x)=|sinx||cosx|,则下列说法正确的是( )A、f(x)的图象关于直线 对称 B、f(x)的周期为 C、(π,0)是f(x)的一个对称中心 D、f(x)在区间 上单调递增12. 将n2个数排成n行n列的一个数阵,如图:该数阵第一列的n个数从上到下构成以m为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列(其中m>0).已知a11=2,a13=a61+1,记这n2个数的和为S.下列结论正确的有( ) A、m=3 B、 C、 D、
A、m=3 B、 C、 D、三、填空题
-
13. 已知向量 (1,1), (﹣1,3), (2,1),且( )∥ ,则λ=.14. (1+ax2)(x﹣3)5的展开式中x7系数为2,则a的值为.15. 双曲线C: 的左、右焦点为F1 , F2 , 直线y b与C的右支相交于点P,若|PF1|=2|PF2|,则双曲线C的离心率为;若该双曲线的焦点到其渐近线的距离是 ,则双曲线的方程为.16. 定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数 的图象向右平移a个单位长度,得到函数h(x)的图象,则h(7)=.
四、解答题
-
17. 现在给出三个条件:①a=2;②B ;③c b.试从中选出两个条件,补充在下面的问题中,使其能够确定△ABC,并以此为依据,求△ABC的面积.
在△ABC中,a、b、c分别是角A、B、C的对边,且满足 ,求△ABC的面积(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)
18. 已知数列{an}的首项为a1=1,且 .(Ⅰ)证明:数列{an+2}是等比数列,并求数列{an}的通项公式;
(Ⅱ)设bn=log2(an+2)﹣log23,求数列 的前n项和 .
19. 如图,在四棱锥P-ABCD中, , 平面PAB, ,点E满足 . (1)、证明: ;(2)、求二面角A-PD-E的余弦值.20. 已知P是圆F1:(x+1)2+y2=16上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.(1)、求曲线C的方程;(2)、记曲线C与x轴交于A,B两点,M是直线x=1上任意一点,直线MA,MB与曲线C的另一个交点分别为D,E,求证:直线DE过定点H(4,0).21. 近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
(1)、证明: ;(2)、求二面角A-PD-E的余弦值.20. 已知P是圆F1:(x+1)2+y2=16上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.(1)、求曲线C的方程;(2)、记曲线C与x轴交于A,B两点,M是直线x=1上任意一点,直线MA,MB与曲线C的另一个交点分别为D,E,求证:直线DE过定点H(4,0).21. 近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:土地使用面积 (单位:亩)
1
2
3
4
5
管理时间 (单位:月)
8
10
13
25
24
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理
不愿意参与管理
男性村民
150
50
女性村民
50
参考公式:
其中 .临界值表:
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
参考数据:
(1)、求出相关系数 的大小,并判断管理时间 与土地使用面积 是否线性相关?(2)、是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?(3)、若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为 ,求 的分布列及数学期望.22. 已知函数 .(1)、求 在点 处的切线方程;(2)、若不等式 恒成立,求k的取值范围;(3)、求证:当 时,不等式 成立.