山东省泰安市肥城市2020届数学一模试卷
试卷更新日期:2020-04-03 类型:高考模拟
一、单选题
-
1. 已知集合A={x|﹣1<x<1},B={x|0<x<2},则A∪B=( )A、(﹣1,2) B、(﹣1,0) C、(0,1) D、(1,2)2. 若集合 ,则“ ”是“ ”的( )A、充分非必要条件 B、必要非充分条件 C、充分必要条件 D、既不充分也非不必要条件3. 已知 , ,若 ,则 的取值范围为( )A、 B、 C、 D、4. 若 , , ,满足 , , ,则( )A、 B、 C、 D、5. 对数函数 且 与二次函数 在同一坐标系内的图象可能是( )A、
 B、
B、 C、
C、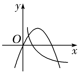 D、
D、 6. 函数 的图象大致是( )A、
6. 函数 的图象大致是( )A、 B、
B、 C、
C、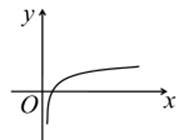 D、
D、 7. 已知函数 ,若 ,那么实数 的值是( )A、4 B、1 C、2 D、38. 2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
7. 已知函数 ,若 ,那么实数 的值是( )A、4 B、1 C、2 D、38. 2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )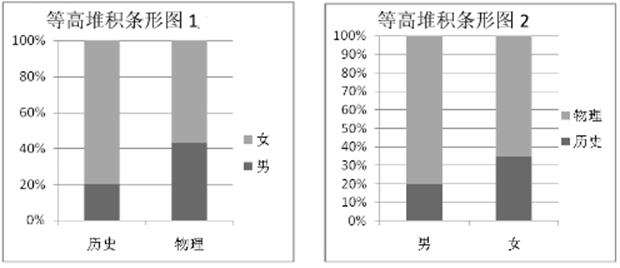 A、样本中的女生数量多于男生数量 B、样本中有学物理意愿的学生数量多于有学历史意愿的学生数量 C、样本中的男生偏爱物理 D、样本中的女生偏爱历史
A、样本中的女生数量多于男生数量 B、样本中有学物理意愿的学生数量多于有学历史意愿的学生数量 C、样本中的男生偏爱物理 D、样本中的女生偏爱历史二、多选题
-
9. 设函数 ,则 ( )A、是偶函数 B、在 单调递减 C、最大值为2 D、其图像关于直线 对称10. 下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类
冰箱类
小家电类
其它类
营业收入占比
90.10%
4.98%
3.82%
1.10%
净利润占比
95.80%
﹣0.48%
3.82%
0.86%
则下列判断中正确的是( )
A、该公司2018年度冰箱类电器销售亏损 B、该公司2018年度小家电类电器营业收入和净利润相同 C、该公司2018年度净利润主要由空调类电器销售提供 D、剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低11. 在空间四边形 中, 分别是 上的点,当 平面 时,下面结论正确的是( )A、 一定是各边的中点 B、 一定是 的中点 C、 ,且 D、四边形 是平行四边形或梯形12. 如图,正方体 的棱长为1,则下列四个命题正确的是( ) A、直线 与平面 所成的角等于 B、点C到面 的距离为 C、两条异面直线 和 所成的角为 D、三棱柱 外接球半径为
A、直线 与平面 所成的角等于 B、点C到面 的距离为 C、两条异面直线 和 所成的角为 D、三棱柱 外接球半径为三、填空题
-
13. .14. 在平面直角坐标系xOy中,将直线l沿x轴正方向平移3个单位长度,沿y轴正方向平移5个单位长度,得到直线l1.再将直线l1沿x轴正方向平移1个单位长度,沿y轴负方向平移2个单位长度,又与直线l重合.若直线l与直线l1关于点(2,3)对称,则直线l的方程是.15. 在我国古代数学名著《九章算术》中,把两底面为直角三角形的直棱柱称为“堑堵”.已知三棱柱 是一个“堑堵”,其中 ,点 是 的中点,则四棱锥 的外接球的表面积为 .16. 定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数 的图象向右平移a个单位长度,得到函数h(x)的图象,则h(7)=.
四、解答题
-
17. 记 为公差不为零的等差数列 的前 项和,已知 , .(1)、求 的通项公式;(2)、求 的最大值及对应 的大小.18. 已知函数(1)、求 的单调递增区间;(2)、求 在 上的最小值及取最小值时的 的集合.19. 如图所示的几何体中, 为三棱柱,且 平面ABC, ,四边形ABCD为平行四边形, , .
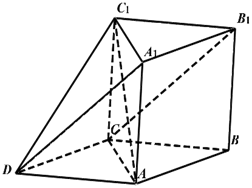 (1)、求证: 平面 ;(2)、若 ,求四棱锥 的体积.20. 在平面直角坐标系 中,已知椭圆 : 的焦距为2,且过点 .(1)、求椭圆 的方程;(2)、设椭圆 的上顶点为 ,右焦点为 ,直线 与椭圆交于 , 两点,问是否存在直线 ,使得 为 的垂心,若存在,求出直线 的方程:若不存在,说明理由.21. 现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如表:
(1)、求证: 平面 ;(2)、若 ,求四棱锥 的体积.20. 在平面直角坐标系 中,已知椭圆 : 的焦距为2,且过点 .(1)、求椭圆 的方程;(2)、设椭圆 的上顶点为 ,右焦点为 ,直线 与椭圆交于 , 两点,问是否存在直线 ,使得 为 的垂心,若存在,求出直线 的方程:若不存在,说明理由.21. 现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如表:月收入(单位百元)
[15,25)
[25,35)
[35,45)
[45,55)
[55,65)
[65,75)
频数
5
10
15
10
5
5
赞成人数
4
8
12
5
2
1
(Ⅰ)由以上统计数据填下面2×2列联表并问是否有99%的把握认为“月收入以5500为分界点”对“楼市限购令”的态度有差异;
月收入低于55百元的人数
月收入不低于55百元的人数
合计
赞成
不赞成
合计
(Ⅱ)若采用分层抽样在月收入在[15,25),[25,35)的被调查人中共随机抽取6人进行追踪调查,并给予其中3人“红包”奖励,求收到“红包”奖励的3人中至少有1人收入在[15,25)的概率.
参考公式:K2 ,其中n=a+b+c+d.
参考数据:
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
22. 已知函数 在 处取得极小值.(1)、求实数 的值;(2)、若函数 存在极大值与极小值,且函数 有两个零点,求实数 的取值范围.(参考数据: , )