辽宁省丹东市2020届高三文数总复习阶段测试试卷
试卷更新日期:2020-04-03 类型:高考模拟
一、单选题
-
1. 复数 等于( )A、 B、 C、 D、2. 已知集合A={x|–1<x<2},B={x|x>1},则A∪B=( )A、(–1,1) B、(1,2) C、(–1,+∞) D、(1,+∞)3. ( )A、 B、 C、 D、4. 从2名男同学,2名女同学共4人中任选2人参加体能测试,则选到的2名同学中恰好有1名男同学的概率是( )A、 B、 C、 D、5. 中, 为 的中点,则( )A、 B、 C、 D、6. 函数 是( )A、奇函数,且在 上是增函数 B、奇函数,且在 上是减函数 C、偶函数,且在 上是增函数 D、偶函数,且在 上是减函数7. 已知两个平面 , 相互垂直, 是它们的交线,则下面结论正确的是( )A、垂直于平面 的平面一定平行于平面 B、垂直于直线 的平面一定平行于平面 C、垂直于平面 的平面一定平行于直线 D、垂直于直线 的平面一定与平面 , 都垂直8. 已知向量 , 满足 , , ,那么 与 的夹角为( )A、 B、 C、 D、9. 函数 在 的图象大致为( )A、
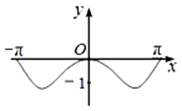 B、
B、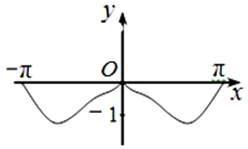 C、
C、 D、
D、 10. “ ”是“ 属于函数 单调递增区间”的( )A、充分不必要条件 B、必要不充分条件 C、充分且必要条件 D、既不充分也不必要条件11. 已知当 时,函数 取得最小值,则 ( )A、 B、 C、 D、12. 已知函数 ,则 的零点个数为( )A、4 B、3 C、2 D、1
10. “ ”是“ 属于函数 单调递增区间”的( )A、充分不必要条件 B、必要不充分条件 C、充分且必要条件 D、既不充分也不必要条件11. 已知当 时,函数 取得最小值,则 ( )A、 B、 C、 D、12. 已知函数 ,则 的零点个数为( )A、4 B、3 C、2 D、1二、填空题
-
13. 已知 是第三象限的角,若 ,则 .14. 已知 为偶函数,当 时, ,则 .15. 中, , , ,则 .16. 边长为2的等边三角形 的三个顶点 , , 都在以 为球心的球面上,若球 的表面积为 ,则三棱锥 的体积为.
三、解答题
-
17. 如图, 是半圆弧 上异于 , 的点,四边形 是矩形, 为 中点.
 (1)、证明: 平面 ;(2)、若矩形 所在平面与半圆弧 所在平面垂直,证明:平面 平面 .18. 某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为 配方和 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
(1)、证明: 平面 ;(2)、若矩形 所在平面与半圆弧 所在平面垂直,证明:平面 平面 .18. 某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为 配方和 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:配方的频数分布表:
指标值分组
[90,94)
[94,98)
[98,102)
[102,106)
[106,110]
频数
8
20
42
22
8
配方的频数分布表:
指标值分组
[90,94)
[94,98)
[98,102)
[102,106]
[106,110]
频数
4
12
42
32
10
(1)、分别估计用 配方、 配方生产的产品的优质品率;(2)、已知用 配方生产的一件产品的利润(单位:元)与其质量指标值 的关系为 ,估计用 配方生产的一件产品的利润大于 的概率,并求用 配方生产的上述 件产品的平均利润.19. 的内角 , , 的对边分别为 , , ,已知 .(1)、求 ;(2)、若 , , 平分线 交 于点 ,求 的长.20. 已知 是定义域为R的奇函数,满足 .(1)、证明: ;(2)、若 ,求式子 的值.21. 已知函数 ,曲线 在 处的切线经过点 .(1)、求实数 的值;(2)、证明: 在 单调递增,在 单调递减;(3)、设 ,求 在 上的最大值和最小值.