江西省南昌市新建二中2020届高三理数模拟试卷 (二)

试卷更新日期：2020-04-03 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $i$ 是虚数单位，则 $\frac{2 i}{1 + i} =$ （）

A、 $1 + i$ B、 $- 1 + i$ C、 $1 - i$ D、 $2 - 2 i$

查看试题解析
2. 已知集合 $A = {x | y = \ln (x + 1)}$ ， $B = {x | 2^{x} - 1 \leq 0}$ ，则 $A \cap B =$ （）

A、 ${x | - 1 < x ⩽ 1}$ B、 ${x | - 1 < x ⩽ 0}$ C、 ${x | 0 < x ⩽ 1}$ D、 ${x | - 1 < x ⩽ 2}$

查看试题解析
3. 若 $\tan x = - \frac{1}{3}$ ，则 $\sin 2 x =$ （）

A、 $\frac{3}{5}$ B、 $- \frac{3}{5}$ C、 $\frac{3}{10}$ D、 $- \frac{3}{10}$

查看试题解析
4. 在 $Δ A B C$ 内部任取一点 $M$ ，使得 $Δ M B C$ 的面积与 $Δ A B C$ 的面积的比值大于 $\frac{1}{3}$ 的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{4}{9}$

查看试题解析
5. 等比数列 ${a_{n}}$ 中， $a_{3} = 6$ ，前三项和 $S_{3} = 18$ ，则公比 $q$ 的值为（）

A、1 B、 $- \frac{1}{2}$ C、1或 $- \frac{1}{2}$ D、－1或 $- \frac{1}{2}$

查看试题解析
6. 执行如图所示的程序框图，输出的结果 $s$ 为（）

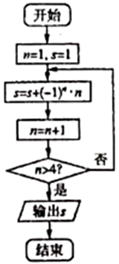A、－2 B、－1 C、2 D、3

查看试题解析
7. 水车是一种利用水流动力进行灌溉的工具，是人类一项古老的发明，也是人类利用自然和改造自然的象征.如图是一个水车的示意图，已知水车逆时针匀速旋转一圈的时间是80秒，半径为3米，水车中心（即圆心）距水面1.5米.若以水面为 $x$ 轴，圆心到水面的垂线为 $y$ 轴建立直角坐标系，水车的一个水斗从出水面点 $A$ 处开始计时，经过 $t$ 秒后转到 $P$ 点的位置，则点 $P$ 到水面的距离 $h$ 与时间 $t$ 的函数关系式为（）

A、 $h = 3 \sin (\frac{π}{40} t - \frac{π}{6}) + 1.5$ B、 $h = 1.5 \cos (\frac{π}{40} t + \frac{π}{6}) + 3$ C、 $h = 3 \cos (\frac{π}{40} t - \frac{π}{3}) + 1.5$ D、 $h = 1.5 \sin (\frac{π}{40} t + \frac{π}{3}) + 3$

查看试题解析
8. 设 $a = {0.2}^{π}$ ， $b = \log_{π} 0.2$ ， $c = π^{0.2}$ ，则（）

A、 $a < c < b$ B、 $a < b < c$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析
9. 五经是指：《诗经》《尚书》《礼记》《周易》《春秋》，记载了我国古代早期思想文化发展史上政治军事、外交、文化等各个方面的史实资料，在中国的传统文化的诸多文学作品中，占据相当重要的位置.学校古典研读社的三名社团学生，到学校图书馆借了一套五经书籍共5本进行研读，若每人至少分一本，则5本书的分配方案种数是（）

A、360 B、240 C、150 D、90

查看试题解析
10. 如图所示是一位学生设计的奖杯模型，奖杯底托为空心的正四面体，且挖去的空心部分是恰好与四面体四个面都相切的球 $O_{1}$ ；顶部为球 $O_{2}$ ，其直径与正四面体的棱长 $a$ 相等，若这样设计奖杯，则球 $O_{1}$ 与球 $O_{2}$ 的半径之比 $r_{1} ： r_{2} =$ （）

A、 $1 ： 6$ B、 $1 ： \sqrt{6}$ C、 $1 ： 3$ D、 $1 ： \sqrt{3}$

查看试题解析
11. 已知圆 $C$ ： $x^{2} + y^{2} - 8 y + 14 = 0$ ，直线 $l$ ： $m x - y - 3 m + 1 = 0$ 与 $x$ 轴， $y$ 轴分别交于 $A$ ， $B$ 两点.设圆 $C$ 上任意一点 $P$ 到直线的距离 $l$ 为 $d$ ，若 $d$ 取最大值时， $Δ P A B$ 的面积（）

A、 $3 \sqrt{2}$ B、8 C、6 D、 $4 \sqrt{2}$

查看试题解析
12. 已知函数 $f (x) = \frac{x \ln x}{a}$ ，若不等式 $f (x) < 2$ 仅有两个整数解，则实数a的取值范围是（）

A、 $[\ln 2 ， \frac{3}{2} \ln 3)$ B、 $[\frac{3}{2} \ln 3 ， 4 \ln 2)$ C、 $(\ln 2 ， \frac{3}{2} \ln 3]$ D、 $(\frac{3}{2} \ln 3 ， 4 \ln 2]$

查看试题解析

二、填空题

13. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 1$ ， $\vec{b} = (1, \sqrt{3})$ ，若 $\vec{a} \cdot (\vec{a} - \vec{b}) = 2$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为.

查看试题解析
14. 一百馒头，一百和尚，大和尚每人每餐a个馒头，小和尚每餐每a人吃1个馒头.若大和尚的人数用 $f (a)$ 表示，则 $f (a) =$ .

查看试题解析
15. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）的左，右焦点分别为 $F_{1}$ ， $F_{2}$ ，过右支上一点 $P$ 作双曲线 $C$ 的一条渐近线的垂线，垂足为 $H$ .若 $| P H | + | P F_{1} |$ 的最小值为 $4 a$ ，则双曲线 $C$ 的离心率为.

查看试题解析
16. 已知数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ 满足： $S_{n} + 2 a_{n} = 6 - 6 \times {(\frac{2}{3})}^{n}$ （ $n \in N *$ ），则数列 ${a_{n}}$ 中最大项等于.

查看试题解析

三、解答题

17. 在 $Δ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，满足 $b c \cos C + c^{2} \cos B = 2 a b$ .

(1)、求 $\frac{c}{b}$ 的值；

(2)、若 $a = \sqrt{6}$ ，则 $Δ A B C$ 的面积的最大值.

查看试题解析
18. 如图，多面体 $A B C E$ 中，平面 $A E C ⊥$ 平面 $A B C$ ， $A C ⊥ B C$ ， $A E ⊥ C D$ 四边形 $B C D E$ 为平行四边形.

(1)、证明： $A E ⊥ E C$ ；

(2)、若 $A E = E C = C B = \sqrt{2}$ ，求二面角 $D - A C - E$ 的余弦值.

查看试题解析
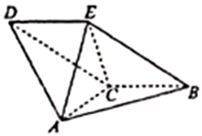19. 已知椭圆 $C_{1}$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）的一个焦点 $F$ 与抛物线 $C_{2}$ ： $y^{2} = 4 x$ 的焦点重合，且离心率为 $\frac{\sqrt{2}}{2}$ .

(1)、求椭圆 $C_{1}$ 的标准方程；

(2)、过焦点 $F$ 的直线 $l$ 与抛物线 $C_{2}$ 交于 $A$ ， $B$ 两点，与椭圆 $C_{1}$ 交于 $C$ ， $D$ 两点，满足 $| A B | = 3 \sqrt{2} | C D |$ ，求直线 $l$ 的方程.

查看试题解析
20. 某城市一社区接到有关部门的通知，对本社区居民用水量进行调研，通过抽样调查的方法获得了100户居民某年的月均用水量（单位：t），通过分组整理数据，得到数据的频率分布直方图如图所示：

（Ⅰ）求图中m的值；并估计该社区居民月均用水量的中位数和平均值.（保留3位小数）

（Ⅱ）用此样本频率估计概率，若从该社区随机抽查3户居民的月均用水量，问恰有2户超过 $2.5 t$ 的概率为多少？

（Ⅲ）若按月均用水量 $[0.5 ， 2.5)$ 和 $[2.5 ， 5.5]$ 分成两个区间用户，按分层抽样的方法抽取10户，每户出一人参加水价调整方案听证会.并从这10人中随机选取3人在会上进行陈述发言，设来自用水量在区间 $[0.5 ， 2.5]$ 的人数为X，求X的分布列和数学期望.

查看试题解析
21. 已知函数 $f (x) = e^{x} - a x + b$ .其中 $a ， b \in R$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、函数 $f (x)$ 在 $x = 0$ 处存在极值－1，且 $x \in (- 1 ， + \infty)$ 时， $f (x) + 2 > k (x + 1)$ 恒成立，求实数 $k$ 的最大整数.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，曲线C的参数方程为： ${\begin{array}{l} x = 2 \cos α \\ y = \sqrt{2} \sin α \end{array}$ （ $α$ 为参数）.在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为 $\sqrt{2} ρ \sin (θ + \frac{π}{4}) = 1$ .
（Ⅰ）求曲线C的普通方程和直线l的直角坐标方程；

（Ⅱ）设点P的直角坐标为 $(1, 0)$ ，若直线l与曲线C分别相交于A，B两点，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x | + | x + 1 |$ .
（Ⅰ）解关于x的不等式 $f (x) \geq 2$ ；

（Ⅱ）若a，b， $c \in R^{+}$ ，函数 $f (x)$ 的最小值为m，若 $a + b + c = m$ ，求证： $a b + b c + a c \leq \frac{1}{3}$ .

查看试题解析