江西名师联盟2020届高三上学期理数第一次模拟考试试卷
试卷更新日期:2020-04-03 类型:高考模拟
一、单选题
-
1. 已知集合 , , ,则 ( )A、 B、 C、 D、2. 若复数 满足 ,则 ( )A、 B、 C、 D、3. 设 是等差数列 的前 项和, , ,则公差 ( )A、 B、 C、1 D、-14. 已知 ,则( )A、 B、 C、 D、5. 函数 的图象大致是( )A、
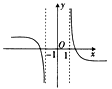 B、
B、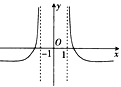 C、
C、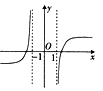 D、
D、 6. 设 满足约束条件 ,则 的最大值是( )A、-1 B、0 C、 D、27. 在 中, , 为 的中点,则 ( )A、 B、 C、 D、8. 若存在 ,使 成立,则 的取值范围为( )A、 B、 C、 D、9. 在直角坐标系 中, 是椭圆 的左焦点, 分别为左、右顶点,过点 作 轴的垂线交椭圆 于 两点,连接 交 轴于点 ,连接 交 于点 ,若 是线段 的中点,则椭圆 的离心率为( )A、 B、 C、 D、10. 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的体积为( )
6. 设 满足约束条件 ,则 的最大值是( )A、-1 B、0 C、 D、27. 在 中, , 为 的中点,则 ( )A、 B、 C、 D、8. 若存在 ,使 成立,则 的取值范围为( )A、 B、 C、 D、9. 在直角坐标系 中, 是椭圆 的左焦点, 分别为左、右顶点,过点 作 轴的垂线交椭圆 于 两点,连接 交 轴于点 ,连接 交 于点 ,若 是线段 的中点,则椭圆 的离心率为( )A、 B、 C、 D、10. 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的体积为( ) A、 B、 C、 D、11. 已知双曲线 (a>0,b>0)的离心率为2,F1 , F2分别是双曲线的左、右焦点,点M(-a,0),N(0,b),点P为线段MN上的动点,当 取得最小值和最大值时,△PF1F2的面积分别为S1 , S2 , 则 =( )A、2 B、4 C、4 D、812. 设函数 在定义域 上是单调函数,且 ,若不等式 对 恒成立,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知双曲线 (a>0,b>0)的离心率为2,F1 , F2分别是双曲线的左、右焦点,点M(-a,0),N(0,b),点P为线段MN上的动点,当 取得最小值和最大值时,△PF1F2的面积分别为S1 , S2 , 则 =( )A、2 B、4 C、4 D、812. 设函数 在定义域 上是单调函数,且 ,若不等式 对 恒成立,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 若 为定义在 上的奇函数,当 时, ,则 .14. 已知 ,则 .15. 已知函数 只有一个零点,则 .16. 在四棱锥 中,底面 为正方形,平面 平面 ,且 为等边三角形,若四棱锥 的体积与四棱锥 外接球的表面积大小之比为 ,则四棱锥 的表面积为.
三、解答题
-
17. 的内角 的对边分别为 ,已知 .(1)、求 ;(2)、若 ,求 的面积.18. 某厂销售部以箱为单位销售某种零件,每箱的定价为 元,低于 箱按原价销售,不低于 箱则有以下两种优惠方案:①以 箱为基准,每多 箱送 箱;②通过双方议价,买方能以优惠 成交的概率为 ,以优惠 成交的概率为 .(1)、甲、乙两单位都要在该厂购买 箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;(2)、某单位需要这种零件 箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?19. 如图所示,在四面体 中, ,平面 平面 , ,且 .
 (1)、证明: 平面 ;(2)、设 为棱 的中点,当四面体 的体积取得最大值时,求二面角 的余弦值.20. 已知椭圆 : 过点 ,且它的焦距是短轴长的 倍.(1)、求椭圆 的方程.(2)、若 , 是椭圆 上的两个动点( , 两点不关于 轴对称), 为坐标原点, , 的斜率分别为 , ,问是否存在非零常数 ,使当 时, 的面积 为定值?若存在,求 的值;若不存在,请说明理由.
(1)、证明: 平面 ;(2)、设 为棱 的中点,当四面体 的体积取得最大值时,求二面角 的余弦值.20. 已知椭圆 : 过点 ,且它的焦距是短轴长的 倍.(1)、求椭圆 的方程.(2)、若 , 是椭圆 上的两个动点( , 两点不关于 轴对称), 为坐标原点, , 的斜率分别为 , ,问是否存在非零常数 ,使当 时, 的面积 为定值?若存在,求 的值;若不存在,请说明理由.