福建省漳州市2020届高三下学期文数（线上)适应性测试试卷

试卷更新日期：2020-04-02 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = {- 1, 0, 1, 2, 3}$ ，集合 $A = {0, 1, 2}$ ， $B = {- 1, 0, 1}$ ，则 $(∁_{U} A) \cap B =$ （）

A、 ${- 1}$ B、 ${0, 1}$ C、 ${- 1, 2, 3}$ D、 ${- 1, 0, 1}$

查看试题解析
2. 已知复数z=2+i，则 $z \cdot \bar{z} =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、3 D、5

查看试题解析
3. 已知非零向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ 满足 $| \overset{⇀}{b} | = 4 | \overset{⇀}{a} |$ ，且 $\overset{⇀}{a} ⊥ (2 \overset{⇀}{a} + \overset{⇀}{b})$ ，则 $\overset{⇀}{a}$ 与 $\overset{⇀}{b}$ 的夹角为（）

A、 $\frac{π}{3}$ B、 $\frac{π}{2}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
4. 已知 ${a_{n}}$ 为等差数列，其公差为-2，且 $a_{7}$ 是 $a_{3}$ 与 $a_{9}$ 的等比中项， $S_{n}$ 为 ${a_{n}}$ 的前n项和， $n \in N^{*}$ ，则 $S_{10}$ 的值为（）

A、-100 B、-90 C、90 D、110

查看试题解析
5. 某公司决定利用随机数表对今年新招聘的800名员工进行抽样调查他们对目前工作的满意程度，先将这800名员工进行编号，编号分别为001，002，…，799，800，从中抽取80名进行调查，下图提供随机数表的第4行到第6行
32 21 18 34 29   78 64 54 07 32   52 42 06 44 38   12 23 43 56 77   35 78 90 56 42

84 42 12 53 31   34 57 86 07 36   25 30 07 32 86   23 45 78 89 07   23 68 96 08 04

32 56 78 08 43   67 89 53 55 77   34 89 94 83 75   22 53 55 78 32   43 77 89 23 45

若从表中第5行第6列开始向右依次读取3个数据，则抽到的第5名员工的编号是（     ）

A、007 B、253 C、328 D、736

查看试题解析
6. 已知双曲线 $C_{1} : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的离心率为 $\sqrt{2}$ ，一条渐近线为l，抛物线 $C_{2} : y^{2} = 4 x$ 的焦点为F，点P为直线l与抛物线 $C_{2}$ 异于原点的交点，则 $| P F | =$ （）

A、3 B、4 C、6 D、5

查看试题解析
7. 函数y= $2^{| x |}$ sin2x的图象可能是

A、 B、 C、 D、

查看试题解析
8. 已知 $α \in R ， \sin α + 2 c o s α = \frac{\sqrt{10}}{2}$ ，则tan2α=（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $- \frac{3}{4}$ D、 $- \frac{4}{3}$

查看试题解析
9. 若 $0 < a < b < 1$ ，则 $a^{b}$ ， $b^{a}$ ， ${log}_{b} a$ ， ${log}_{\frac{1}{a}} b$ 的大小关系为（）

A、 $a^{b} > b^{a} > {log}_{b} a > {log}_{\frac{1}{a}} b$ B、 $b^{a} > a^{b} > {log}_{\frac{1}{a}} b > {log}_{b} a$ C、 ${log}_{b} a > a^{b} > b^{a} > {log}_{\frac{1}{a}} b$ D、 ${log}_{b} a > b^{a} > a^{b} > {log}_{\frac{1}{a}} b$

查看试题解析
10. 中国古代近似计算方法源远流长，早在八世纪，我国著名数学家、天文学家张隧（法号：一行）为编制《大衍历》发明了一种近似计算的方法——二次插值算法（又称一行算法，牛顿也创造了此算法，但是比我国张隧晚了上千年）：对于函数 $y = f (x)$ ，若 $y_{1} = f (x_{1}),$ $y_{2} = f (x_{2}),$ $y_{3} = f (x_{3}),$ $x_{1} < x_{2} < x_{3}$ ，则在区间 $[x_{1}, x_{3}]$ 上 $f (x)$ 可以用二次函数 $f (x) = y_{1} + k_{1} (x - x_{1}) + k_{2} (x - x_{1}) (x - x_{2})$ 来近似代替，其中 $k_{1} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}},$ $k = \frac{y_{3} - y_{2}}{x_{3} - x_{2}}$ ， $k_{2} = \frac{k - k_{1}}{x_{3} - x_{1}}$ ，若令 $x_{1} = 0,$ $x_{2} = \frac{π}{2},$ $x_{3} = π$ ，请依据上述算法，估算 $\sin \frac{2 π}{5}$ 的近似值是（）

A、 $\frac{24}{25}$ B、 $\frac{17}{25}$ C、 $\frac{16}{25}$ D、 $\frac{4}{5}$

查看试题解析
11. 在 $△ A B C$ 中，D是边AC上的点，且 $A B = A D ，$ $2 A B = \sqrt{3} B D ，$ $B C = 2 B D$ ，则 $\sin C$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{\sqrt{6}}{4}$ D、 $\frac{\sqrt{6}}{6}$

查看试题解析
12. 已知正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面边长为1，高为2，M为 $B_{1} C_{1}$ 的中点，过M作平面 $α$ ，使得平面 $α //$ 平面 $A_{1} B D$ ，若平面 $α$ 把 $A B C - A_{1} B_{1} C_{1}$ 分成的两个几何体中，体积较小的几何体的体积为（）

A、 $\frac{1}{48}$ B、 $\frac{1}{24}$ C、 $\frac{1}{12}$ D、 $\frac{1}{8}$

查看试题解析

二、填空题

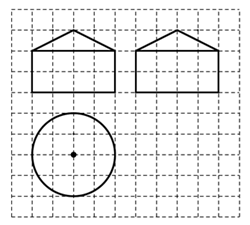
13. 若曲线 $C : x^{2} + y^{2} - 6 x + 10 y + a = 0$ 上存在不同的两点关于直线 $y = k x + 7$ 对称，则 $k =$ ．

查看试题解析
14. 若函数 $f (x)$ 是定义在R上的偶函数，且 $f (x + 4) = - f (x)$ ，当 $x \in (0, 2)$ 时， $f (x) = \ln x + x + 1$ ，则当 $x \in (6, 8)$ 时， $f (x) =$ ．

查看试题解析
15. 如图，小方格是边长为1的正方形，图中粗线画出的是某几何体的三视图，该几何体是由一个圆锥和一个圆柱组成，若在这个几何体内任取一点，则该点取自圆锥内的概率为．

查看试题解析
16. 已知P是曲线 $C_{1} ： y = x^{3} - x (- \frac{3}{2} \leq x \leq \frac{3}{2})$ 上的点，Q是曲线 $C_{2}$ 上的点，曲线 $C_{1}$ 与曲线 $C_{2}$ 关于直线 $y = 2 x + 4$ 对称，M为线段PQ的中点，O为坐标原点，则 $| O M |$ 的最小值为．

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ,且 $S_{n} = 2 n^{2} + n$ , $n \in N^{*}$ ,数列 ${b_{n}}$ 满足 $a_{n} = 4 \log_{2} b_{n} + 3$ ， $n \in N^{*}$ .

(1)、求 $a_{n}$ 和 $b_{n}$ 的通项公式；

(2)、求数列{ $a_{n} \cdot b_{n}$ }的前n项和 $T_{n}$ .

查看试题解析
18. 如图，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的底面是正三角形， $A A_{1} ⊥$ 底面 $A_{1} B_{1} C_{1}$ ，M为 $A_{1} B_{1}$ 的中点．

(1)、求证： $B_{1} C / /$ 平面 $A M C_{1}$ ；

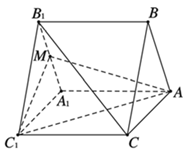(2)、若 $B B_{1} = 4$ ，且沿侧棱 $B B_{1}$ 展开三棱柱的侧面，得到的侧面展开图的对角线长为 $4 \sqrt{10}$ ，求作点 $A_{1}$ 在平面 $A M C_{1}$ 内的射影H，请说明作法和理由，并求线段AH的长．

查看试题解析
19. 某保险公司有一款保险产品的历史收益率（收益率 $=$ 利润 $\div$ 保费收入）的频率分布直方图如图所示：

(1)、试估计这款保险产品的收益率的平均值；

(2)、设每份保单的保费在20元的基础上每增加 $x$ 元，对应的销量为 $y$ （万份）．从历史销售记录中抽样得到如下5组 $x$ 与 $y$ 的对应数据：

$x$ 元

25

30

38

45

52

销量为 $y$ （万份）

7.5

7.1

6.0

5.6

4.8

由上表，知 $x$ 与 $y$ 有较强的线性相关关系，且据此计算出的回归方程为 $\hat{y} = 10.0 - b x$ ．

（ⅰ）求参数 $b$ 的值；

（ⅱ）若把回归方程 $\hat{y} = 10.0 - b x$ 当作 $y$ 与 $x$ 的线性关系，用（1）中求出的收益率的平均值作为此产品的收益率，试问每份保单的保费定为多少元时此产品可获得最大利润，并求出最大利润．注：保险产品的保费收入 $=$ 每份保单的保费 $\times$ 销量．

查看试题解析
20. 已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个焦点为 $F (1, 0)$ ，且 $(- 1, \frac{\sqrt{2}}{2})$ 在椭圆E上．

(1)、求椭圆E的标准方程；

(2)、已知垂直于x轴的直线 $l_{1}$ 交E于A、B两点，垂直于y轴的直线 $l_{2}$ 交E于C、D两点， $l_{1}$ 与 $l_{2}$ 的交点为P，且 $| A B | = | C D |$ ，间：是否存在两定点M，N，使得 $| | P M | - | P N | |$ 为定值？若存在，求出M，N的坐标，若不存在，请说明理由．

查看试题解析
21. 已知函数 $f (x) = e^{x} - \ln x$ ，定义在 $(0 ， + \infty)$ 上的函数 $g (x)$ 的导函数 $g^{'} (x) = (e^{x} - a) (\ln x - a)$ ，其中 $a \in R$ ．

(1)、求证： $f (x) > 0$ ；

(2)、求函数 $g (x)$ 的单调区间．

查看试题解析
22. 在直角坐标系xOy下，曲线C₁的参数方程为 ${\begin{array}{l} x = \cos α ， \\ y = \sin α \end{array}$ （ $α$ 为参数），曲线C₁在变换T： ${\begin{array}{l} x^{'} = 2 x \\ y^{'} = y \end{array}$ 的作用下变成曲线C₂ ．

(1)、求曲线C₂的普通方程；

(2)、若m>1，求曲线C₂与曲线C₃：y=m|x|-m的公共点的个数．

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | 3 x + 1 | - m$ ．

(1)、当 $m = 5$ 时，求不等式 $f (x) > 0$ 的解集；

(2)、若当 $x \neq \frac{1}{4}$ 时，不等式 $f (x) + \frac{16}{| 4 x - 1 |} > 0$ 恒成立，求实数m的取值范围．

查看试题解析

$x$ 元	25	30	38	45	52
销量为 $y$ （万份）	7.5	7.1	6.0	5.6	4.8