福建省厦门市2020届理数高三毕业班第一次质量检测试卷

试卷更新日期：2020-04-02 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $A = {x | | x | \leq 1}$ ， $B = {x | {(x - \frac{1}{2})}^{2} \leq 0}$ ，则 $A \cap C_{R} B =$ （）

A、 $[- 1, 1]$ B、 $ϕ$ C、 $[- 1, \frac{1}{2}) \cup (\frac{1}{2}, 1]$ D、 $(- 1, 1)$

查看试题解析
2. 设 $z = - i + 3$ ，则 $\bar{z} + | \bar{z} | =$ （）

A、 $i - 3 + \sqrt{10}$ B、 $i + 3 + \sqrt{10}$ C、 $- i + 3 + \sqrt{10}$ D、 $- i - 3 + \sqrt{10}$

查看试题解析

3. 中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐，奖牌榜的前3名如下：

国家	金牌	银牌	铜牌	奖牌总数
中国	133	64	42	239
俄罗斯	51	53	57	161
巴西	21	31	36	88

某数学爱好者采用分层抽样的方式，从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人，则这3人中中国选手恰好1人的概率为（）

A、

\frac{22}{57}

B、

\frac{19}{1540}

C、

\frac{57}{1540}

D、

\frac{171}{1540}

查看试题解析

4. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，公差为-2，且 $a_{7}$ 是 $a_{3}$ 与 $a_{9}$ 的等比中项，则 $S_{10}$ 的值为（）

A、－110 B、－90 C、90 D、110

查看试题解析
5. 已知函数 $f (x) = e^{x} + e^{- x}$ ，给出以下四个结论：
⑴ $f (x)$ 是偶函数；

⑵ $f (x)$ 的最大值为2；

⑶当 $f (x)$ 取到最小值时对应的 $x = 0$ ；

⑷ $f (x)$ 在 $(- \infty, 0)$ 单调递增，在 $(0, + \infty)$ 单调递减.

正确的结论是（）

A、⑴ B、⑴⑵⑷ C、⑴⑶ D、⑴⑷

查看试题解析
6. 已知正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面边长为1，高为2， $M$ 为 $B_{1} C_{1}$ 的中点，过 $M$ 作平面 $α$ 平行平面 $A_{1} B D$ ，若平面 $α$ 把该正四棱柱分成两个几何体，则体积较小的几何体的体积为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{16}$ C、 $\frac{1}{24}$ D、 $\frac{1}{48}$

查看试题解析
7. 设 $a = e^{- \frac{1}{2}}$ ， $b = 4 e^{- 2}$ ， $c = 2 e^{- 1}$ ， $d = 3 e^{- \frac{3}{2}}$ ，则 $a, b, c, d$ 的大小关系为（）

A、 $c > b > d > a$ B、 $c > d > a > b$ C、 $c > b > a > d$ D、 $c > d > b > a$ .

查看试题解析
8. 函数 $f (x) = \sin x \cdot | \cos x |$ 的最小正周期与最大值之比为（）

A、 $π$ B、 $2 π$ C、 $4 π$ D、 $8 π$

查看试题解析
9. 已知三角形 $A B C$ 为直角三角形，点 $E$ 为斜边 $A B$ 的中点，对于线段 $A B$ 上的任意一点 $D$ 都有 $\overset{⇀}{C E} \cdot \overset{⇀}{C D} = | \overset{⇀}{B C} + \overset{⇀}{A C} | = 4$ ，则 $| \vec{C D} |$ 的取值范围是（）

A、 $[2, 2 \sqrt{6}]$ B、 $[2, 2 \sqrt{6})$ C、 $[2, 2 \sqrt{2}]$ D、 $[2, 2 \sqrt{2})$

查看试题解析
10. 中国古代近似计算方法源远流长，早在八世纪，我国著名数学家、天文学家张隧（法号：一行）为编制《大衍历》发明了一种近似计算的方法——二次插值算法（又称一行算法，牛顿也创造了此算法，但是比我国张隧晚了上千年）：对于函数 $y = f (x)$ 在 $x_{1}, x_{2}, x_{3} (x_{1} < x_{2} < x_{3})$ 处的函数值分别为 $y_{1} = f (x_{1}), y_{2} = f (x_{2}), y_{3} = f (x_{3})$ ，则在区间 $[x_{1}, x_{3}]$ 上 $f (x)$ 可以用二次函数 $f (x) = y_{1} + k_{1} (x - x_{1}) + k_{2} (x - x_{1}) (x - x_{2})$ 来近似代替，其中 $k_{1} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}, k = \frac{y_{3} - y_{2}}{x_{3} - x_{2}}, k_{2} = \frac{k - k_{1}}{x_{3} - x_{1}}$ .若令 $x_{1} = 0$ ， $x_{2} = \frac{π}{2}$ ， $x_{3} = π$ ，请依据上述算法，估算 $\sin \frac{2 π}{5}$ 的近似值是（）

A、 $\frac{24}{25}$ B、 $\frac{17}{25}$ C、 $\frac{16}{25}$ D、 $\frac{3}{5}$

查看试题解析
11. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的右支与抛物线 $x^{2} = 2 p y$ 相交于 $A, B$ 两点，记点 $A$ 到抛物线焦点的距离为 $d_{1}$ ，抛物线的准线到抛物线焦点的距离为 $d_{2}$ ，点 $B$ 到抛物线焦点的距离为 $d_{3}$ ，且 $d_{1}, d_{2}, d_{3}$ 构成等差数列，则双曲线的渐近线方程为（）

A、 $y = \pm \frac{\sqrt{2}}{2} x$ B、 $y = \pm \sqrt{2} x$ C、 $y = \pm \sqrt{3} x$ D、 $y = \pm \frac{\sqrt{3}}{3} x$

查看试题解析
12. 已知方程 $x e^{x} - a (e^{2 x} - 1) = 0$ 只有一个实数根，则 $a$ 的取值范围是（）

A、 $a \leq 0$ 或 $a \geq \frac{1}{2}$ B、 $a \leq 0$ 或 $a \geq \frac{1}{3}$ C、 $a \leq 0$ D、 $a \geq 0$ 或 $a \leq - \frac{1}{3}$

查看试题解析

二、填空题

13. ${(2 x + 3 y)}^{4}$ 的展开式中二项式系数最大的项为 .

查看试题解析
14. 高三年段有四个老师分别为 $a, b, c, d$ ，这四位老师要去监考四个班级 $A, B, C, D$ ，每个老师只能监考一个班级，一个班级只能有一个监考老师.现要求 $a$ 老师不能监考 $A$ 班， $b$ 老师不能监考 $B$ 班， $c$ 老师不能监考 $C$ 班， $d$ 老师不能监考 $D$ 班，则不同的监考方式有种.

查看试题解析
15. 已知圆 $O$ ： $x^{2} + y^{2} = 1$ ，圆 $N$ ： ${(x - a + 2)}^{2} + {(y - a)}^{2} = 1$ . 若圆 $N$ 上存在点 $Q$ ，过点 $Q$ 作圆 $O$ 的两条切线. 切点为 $A, B$ ，使得 $∠ A Q B = 60^{\circ}$ ，则实数 $a$ 的取值范围是

查看试题解析
16. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为3. 点 $N$ 是棱 $A_{1} B_{1}$ 的中点，点 $T$ 是棱 $C C_{1}$ 上靠近点 $C$ 的三等分点. 动点 $Q$ 在正方形 $D_{1} D A A_{1}$ (包含边界)内运动，且 $Q B / /$ 面 $D_{1} N T$ ，则动点 $Q$ 所形成的轨迹的长度为

查看试题解析

三、解答题

17. 已知函数 $f (x) = \sin x (\cos x - \sin x) + \frac{1}{2}$ .

(1)、求 $f (x)$ 的单调递减区间；

(2)、在锐角 $△ A B C$ 中， $a$ ， $b$ ， $c$ 分别为角 $A$ ， $B$ ， $C$ 的对边，且满足 $a \cos 2 B = a \cos B - b \sin A$ ，求 $f (A)$ 的取值范围.

查看试题解析
18. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，已知 $A B = A C = A A_{1} = \sqrt{5}$ ， $B C = 4$ ， $O$ 为 $B C$ 的中点， $A_{1} O ⊥$ 平面 $A B C$

(1)、证明四边形 $B B_{1} C_{1} C$ 为矩形；

(2)、求直线 $A A_{1}$ 与平面 $A_{1} B_{1} C$ 所成角的余弦值.

查看试题解析
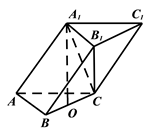19. 根据养殖规模与以往的养殖经验，某海鲜商家的海产品每只质量（克）在正常环境下服从正态分布 $N (280, 25)$ ．
附：若随机变量 $Z ～ N (1, 4)$ ，则 $P (- 5 < Z < 7) = 0.9974$ ， ${0.9987}^{10} \approx 0.9871$ ；

对于一组数据 $(u_{1}, v_{1})$ ， $(u_{2}, v_{2})$ ， $\cdot \cdot \cdot$ ， $(u_{n}, v_{n})$ ，其回归线 $v = α + β u$ 的斜率和截距的最小二乘估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}}$ ， $\hat{α} = \bar{v} - \hat{β} \bar{u}$ ．

(1)、随机购买10只该商家的海产品，求至少买到一只质量小于 $265$ 克该海产品的概率．

(2)、2020年该商家考虑增加先进养殖技术投入，该商家欲预测先进养殖技术投入为49千元时的年收益增量．现用以往的先进养殖技术投入 $x_{i}$ （千元）与年收益增量 $y_{i}$ （千元）（ $i = 1, 2, 3, \cdot \cdot \cdot, 8$ ）的数据绘制散点图，由散点图的样本点分布，可以认为样本点集中在曲线 $y = a + b \sqrt{x}$ 的附近，且 $\bar{x} = 46.6$ ， $\bar{y} = 563$ ， $\bar{t} = 6.8$ ， $\sum_{i = 1}^{8} {(x_{i} - \bar{x})}^{2} = 289.8$ ， $\sum_{i = 1}^{8} {(t_{i} - \bar{t})}^{2} = 1.6$ ， $\sum_{8}^{i = 1} (x_{i} - \bar{x}) (y_{i} - \bar{y}) = 1469$ ， $\sum_{i = 1}^{8} (t_{i} - \bar{t}) (y_{i} - \bar{y}) = 108.8$ ，其中 $t_{i} = \sqrt{x_{i}}$ ， $\bar{t}$ = $\frac{1}{8}$ $\sum_{i = 1}^{8} t_{i}$ ．根据所给的统计量，求 $y$ 关于 $x$ 的回归方程，并预测先进养殖技术投入为49千元时的年收益增量．

查看试题解析
20. 在平面直角坐标系 $x O y$ 中，圆 $A : {(x - 1)}^{2} + y^{2} = 16$ ，点 $B (- 1, 0)$ ，过 $B$ 的直线 $l$ 与圆 $A$ 交于点 $C, D$ ，过 $B$ 做直线 $B E$ 平行 $A C$ 交 $A D$ 于点 $E$ ．

(1)、求点 $E$ 的轨迹 $τ$ 的方程；

(2)、过 $A$ 的直线与 $τ$ 交于 $H$ 、 $G$ 两点，若线段 $H G$ 的中点为 $M$ ，且 $\vec{M N} = 2 \vec{O M}$ ，求四边形 $O H N G$ 面积的最大值．

查看试题解析
21. 已知函数 $f (x) = l n x + a x + 1$ 有两个零点 $x_{1} ， x_{2}$ .

(1)、求 $a$ 的取值范围；

(2)、记 $f (x)$ 的极值点为 $x_{0}$ ，求证： $x_{1} + x_{2} > 2 e f (x_{0})$ .

查看试题解析
22. 在直角坐标系xOy下，曲线C₁的参数方程为 ${\begin{array}{l} x = \cos α ， \\ y = \sin α \end{array}$ （ $α$ 为参数），曲线C₁在变换T： ${\begin{array}{l} x^{'} = 2 x \\ y^{'} = y \end{array}$ 的作用下变成曲线C₂ ．

(1)、求曲线C₂的普通方程；

(2)、若m>1，求曲线C₂与曲线C₃：y=m|x|-m的公共点的个数．

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | 3 x + 1 | - m$ ．

(1)、当 $m = 5$ 时，求不等式 $f (x) > 0$ 的解集；

(2)、若当 $x \neq \frac{1}{4}$ 时，不等式 $f (x) + \frac{16}{| 4 x - 1 |} > 0$ 恒成立，求实数m的取值范围．

查看试题解析