安徽省淮南市2020届高三文数第一次模拟考试试卷
试卷更新日期:2020-04-02 类型:高考模拟
一、单选题
-
1. 若集合 , ,则 ( )A、 B、 C、 D、2. 已知 , 为虚数单位,若复数 是纯虚数,则a的值为( )A、 B、0 C、1 D、23. 已知a,b都是实数,那么“ ”是“ ”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件4. 函数 零点的个数是( )A、0 B、1 C、2 D、35. 由下表可计算出变量 的线性回归方程为( )
5
4
3
2
1
2
1.5
1
1
0.5
A、 B、 C、 D、6. 数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知 的顶点 , ,且 ,则 的欧拉线方程为( )A、 B、 C、 D、7. 函数 的大致图象为( )A、 B、
B、 C、
C、 D、
D、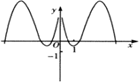 8. 在 中, , ,点 为 的外心,则 的值为( )A、26 B、13 C、 D、109. 已知数列 满足 ,且 是函数 的极值点,设 ,记 表示不超过 的最大整数,则 ( )A、2019 B、2018 C、1009 D、100810. 如图,一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为5 cm,如果不计容器的厚度,则球的表面积为( )
8. 在 中, , ,点 为 的外心,则 的值为( )A、26 B、13 C、 D、109. 已知数列 满足 ,且 是函数 的极值点,设 ,记 表示不超过 的最大整数,则 ( )A、2019 B、2018 C、1009 D、100810. 如图,一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为5 cm,如果不计容器的厚度,则球的表面积为( ) A、 B、 C、 D、11. 已知双曲线 的左右焦点分别为 、 ,过点 的直线交双曲线右支于 、 两点,若 是等腰三角形,且 .则 的周长为( )A、 B、 C、 D、12. 若函数 有三个不同的零点,则实数a的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知双曲线 的左右焦点分别为 、 ,过点 的直线交双曲线右支于 、 两点,若 是等腰三角形,且 .则 的周长为( )A、 B、 C、 D、12. 若函数 有三个不同的零点,则实数a的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 若实数x,y满足 则 的最大值为 .14. 已知 , ,则 的值为 .15. 已知函数 ,满足 (a,b均为正实数),则ab的最大值为 .16. 设抛物线 的焦点为F,过点F的直线l与抛物线交于A,B两点,且 ,则弦长 .
三、解答题
-
17. 在 中,角A,B,C的对边分别为a,b,c, .
(Ⅰ)求角C的大小;
(Ⅱ)已知点P在边BC上, , , ,求 的面积.
18. 高铁、移动支付、网购与共享单车被称为中国的新四大发明,为了解永安共享单车在淮南市的使用情况,永安公司调查了100辆共享单车每天使用时间的情况,得到了如图所示的频率分布直方图.
(Ⅰ)求图中 的值;
(Ⅱ)现在用分层抽样的方法从前3组中随机抽取8辆永安共享单车,将该样本看成一个总体,从中随机抽取2辆,求其中恰有1辆的使用时间不低于50分钟的概率;
(Ⅲ)为进一步了解淮南市对永安共享单车的使用情况,永安公司随机抽取了200人进行调查问卷分析,得到如下2×2列联表:
经常使用
偶尔使用或不用
合计
男性
50
100
女性
40
合计
200
完成上述2×2列联表,并根据表中的数据判断是否有85%的把握认为淮南市使用永安共享单车的情况与性别有关?
附:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
19. 如图在梯形 中, , , 为 的中点 ,以 为折痕把 折起,使点 到达点 的位置,且 .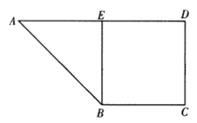

(Ⅰ)求证: 平面 ;
(Ⅱ)设 , 分别为 , 的中点,求三棱锥 的体积.
20. 已知椭圆 的离心率为 , , 分别是椭圆的左右焦点,过点 的直线交椭圆于 , 两点,且 的周长为12.(Ⅰ)求椭圆 的方程
(Ⅱ)过点 作斜率为 的直线 与椭圆 交于两点 , ,试判断在 轴上是否存在点 ,使得 是以 为底边的等腰三角形若存在,求点 横坐标的取值范围,若不存在,请说明理由.