山东省枣庄市峄城区2018-2019学年九年级下学期数学3月月考试卷

试卷更新日期：2020-04-02 类型：月考试卷

进入出卷网下载

一、选择题：（3×12）

1. 若关于的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，则m的取值范围是（）

A、 $m < - 1$ B、 $m < 1$ C、 $m > - 1$ D、 $m > 1$

查看试题解析
2. x₁、x₂是一元二次方程3（x﹣1）²=15的两个解，且x₁＜x₂ ，下列说法正确的是（）

A、x₁小于﹣1，x₂大于3 B、x₁小于﹣2，x₂大于3 C、x₁ ， x₂在﹣1和3之间 D、x₁ ， x₂都小于3

查看试题解析
3. 已知关于x的方程x²+3x+a=0有一个根为﹣2，则另一个根为（　　）

A、5 B、﹣1 C、2 D、﹣5

查看试题解析
4. 已知关于x的一元二次方程x²+mx+n=0的两个实数根分别为x₁=﹣2，x₂=4，则m+n的值是（）

A、﹣10 B、10 C、﹣6 D、2

查看试题解析
5. 将一次函数y= $\frac{1}{2}$ x的图象向上平移2个单位，平移后，若y＞0，则x的取值范围是（）

A、x＞4 B、x＞﹣4 C、x＞2 D、x＞﹣2

查看试题解析
6.
如图是由6个相同的小正方体组成的几何体，那么这个几何体的俯视图是（　　）

A、 B、 C、 D、

查看试题解析
7. 将抛物线 $y = 3 x^{2}$ 向左平移2个单位，再向下平移1个单位，所得抛物线为（）

A、 $y = 3 {(x - 2)}^{2} - 1$ B、 $y = 3 {(x - 2)}^{2} + 1$ C、 $y = 3 {(x + 2)}^{2} - 1$ D、 $y = 3 {(x + 2)}^{2} + 1$

查看试题解析
8. 已知二次函数y=ax²+bx+c的x、y的部分对应值如下表：
x
﹣1
0
1
2
3
y
5
1
﹣1
﹣1
1
则该二次函数图象的对称轴为（）

A、y轴 B、直线x= $\frac{5}{2}$ C、直线x=2 D、直线x= $\frac{3}{2}$

查看试题解析
9. 如图是二次函数y=ax²+bx+c（a≠0）图象的一部分，对称轴为x= $\frac{1}{2}$ ，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y₁），（1，y₂）是抛物线上的两点，则y₁=y₂ ．上述说法正确的是（）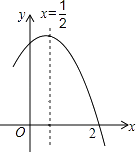

A、①②④ B、③④ C、①③④ D、①②

查看试题解析
10.
如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2 $\sqrt{3}$ ，则阴影部分的面积为（　　）

A、2π B、π C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
11. 如图，已知线段OA交⊙O于点B ，且OB＝AB ，点P是⊙O上的一个动点，那么∠OAP的最大值是

A、90° B、60° C、45° D、30°

查看试题解析
12. 如图，O是坐标原点，菱形OABC的顶点A的坐标为（﹣3，4），顶点C在x轴的负半轴上，函数y= $\frac{k}{x}$ （x＜0）的图象经过顶点B，则k的值为（）

A、﹣12 B、﹣27 C、﹣32 D、﹣36

查看试题解析

二、填空题（4×6）

13. 一个长为a宽为b的长方形黑板，用半径为1的圆形黑板擦，擦不到的面积为。

查看试题解析
14. 如图，将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处．若AE= $\frac{2}{3}$ BE，则长AD与宽AB的比值是．

查看试题解析
15. 如图，一个边长为4cm的等边三角形ABC的高与⊙O的直径相等．⊙O与BC相切于点C，与AC相交于点E，则CE的长为.

查看试题解析
16. 如图，已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b，④4ac﹣b²＜0；其中正确的结论有序号是.

查看试题解析
17.
如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为米（结果精确到0.1米，参考数据： $\sqrt{2}$ =1.41， $\sqrt{3}$ =1.73）．

查看试题解析
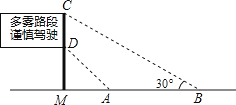18.
如图，在半径为3的⊙O中，直径AB与弦CD相交于点E，连接AC，BD，若AC=2，则tanD= ．

查看试题解析

三、解答题

19. 计算： $| \sqrt{3} - 2 | + \sin 60 ° - \sqrt{27} - {(- 1 \frac{1}{2})}^{2} + 2^{- 2}$

查看试题解析
20. 交通安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使 $∠ C A D = 30^{\circ}$ ， $∠ C B D = 60^{\circ}$ ．

(1)、求AB的长（精确到0.1米，参考数据： $\sqrt{3} = 1.73$ ， $\sqrt{2} = 1.41$ ）；

(2)、已知本路段对汽车限速为40千米/小时，若测得某辆汽车从A到B用时为2秒，这辆汽车是否超速？说明理由．

查看试题解析
21. 如图，AB是⊙O的直径，AC是弦，直线EF经过点C， $A D ⊥ E F$ 于点D， $∠ D A C = ∠ B A C$

(1)、求证：EF是⊙O的切线；

(2)、求证： $A C^{2} = A D \cdot A B$ ；

(3)、若⊙O的半径为2， $∠ A C D = 30^{\circ}$ ，求图中阴影部分的面积．

查看试题解析
22.
如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．

(1)、判断DE与⊙O的位置关系，并说明理由；

(2)、求证：BC²=CD•2OE；

(3)、若cos∠BAD= $\frac{3}{5}$ ， BE=6，求OE的长．

查看试题解析
23. 如图，已知抛物线y=x²+bx+c经过点A（3，0），B（1，0），交y轴于点C，P是抛物线上一动点，点P从点C沿抛物线向A点运动（点P不与点A重合），过点P作PD∥y轴交直线AC于点D

(1)、求二次函数解析式；

(2)、求线段PD长度的最大值；

(3)、在抛物线的对称轴上是否存在点M，使 $| M A - M C |$ 最大？若存在，求出点M的坐标；若不存在请说明理由

查看试题解析
24. 如图，在平面直角坐标系中，二次函数 $y = x^{2} + b x + c$ 的图象与x轴交于A、B两点，B点的坐标为(3，0)，与y轴交于点 $C (0 ， - 3)$ ，点P是直线BC下方抛物线上的一个动点．

(1)、求二次函数解析式；

(2)、连接PO ， PC ，并将△POC沿y轴对折，得到四边形 $P O P^{'} C$ .是否存在点P ，使四边形 $P O P^{'} C$ 为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；

(3)、当点P运动到什么位置时，△PBC的面积最大？求出此时P点的坐标和三角形的最大面积.

查看试题解析

x	﹣1	0	1	2	3
y	5	1	﹣1	﹣1	1